A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
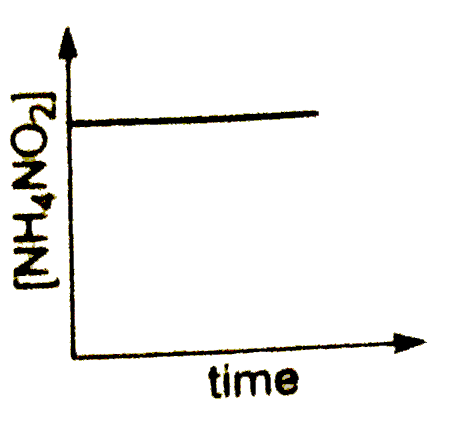
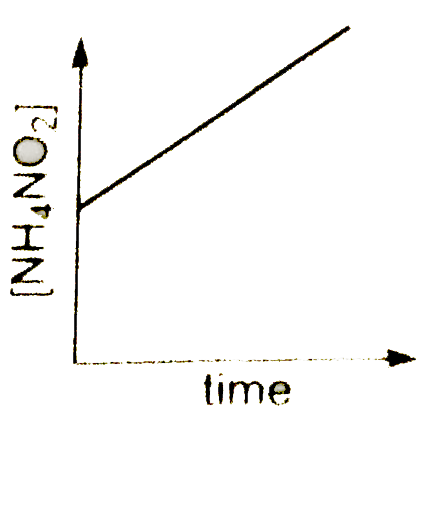
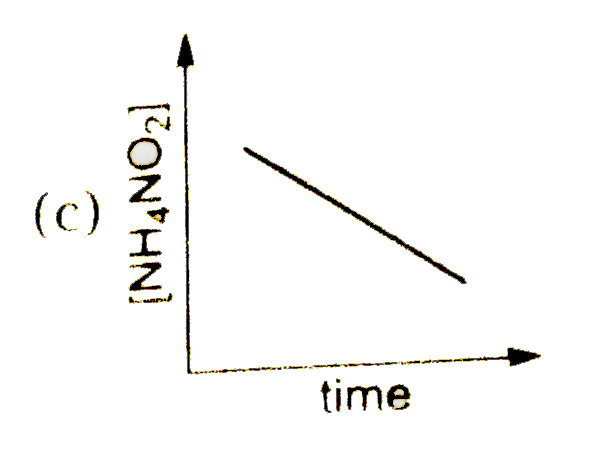
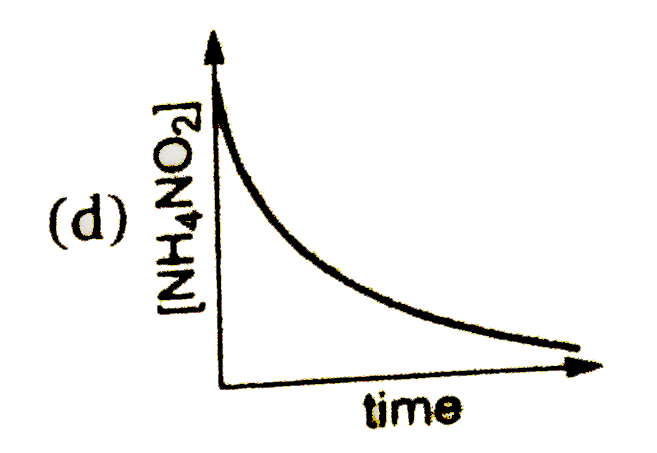
- Decomposition of NH(4)NO(2)(aq into N(2)(g) and 2H(2)O(l) is first ord...
Text Solution
|
- The half time of first order decomposition of nitramide is 2.1 hour at...
Text Solution
|
- For the reaction, N(2)H(4)(l) to N(2)(g) + 2H(2)(g) DeltaH^(@) =-50....
Text Solution
|
- Decomposition of NH(4)NO(2)(aq into N(2)(g) and 2H(2)O(l) is first ord...
Text Solution
|
- The equilibrium constant for the reaction NH(4)NO(2)(s)hArr N(2)(g)+2H...
Text Solution
|
- For the first order reaction 2 N(2)O(5)(g) to 4 NO(2) (g) + O(2)(g)
Text Solution
|
- निम्नलिखित अभिक्रियाओं में ऑक्सीकृत , अपचयित ऑक्सीकारक तथा अपचायक पदार...
Text Solution
|
- Select the correct statement about the following reactions. NH(4) + NO...
Text Solution
|
- Observe the following reaction, 2NO(2)(g) + 2OH^(-)(aq) to NO(3)^(-)(a...
Text Solution
|