Select the incorrect graph for velocity of `e^(-)` in an orbit vs. Z, `1/n` and n :
Select the incorrect graph for velocity of `e^(-)` in an orbit vs. Z, `1/n` and n :
A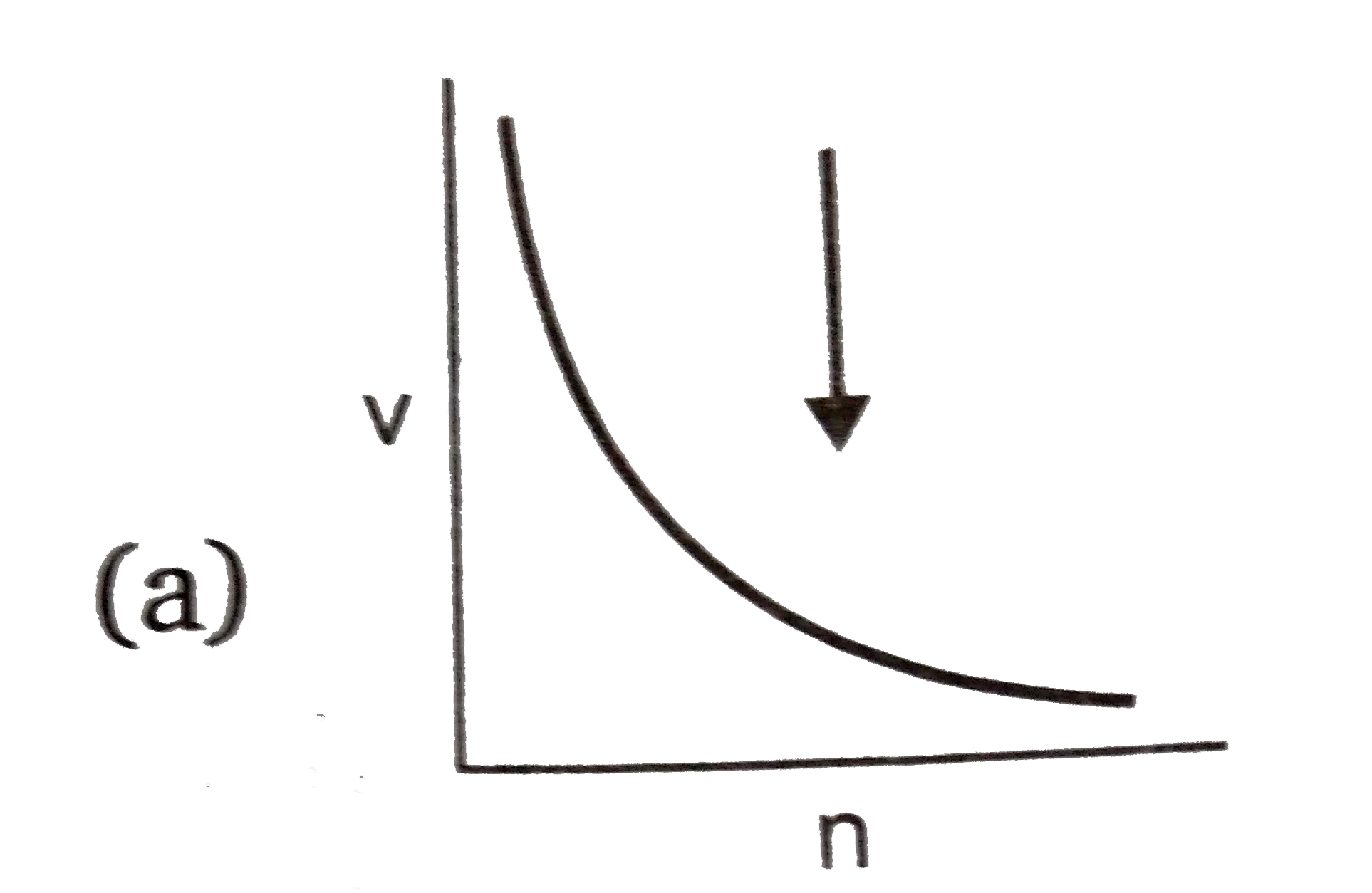

B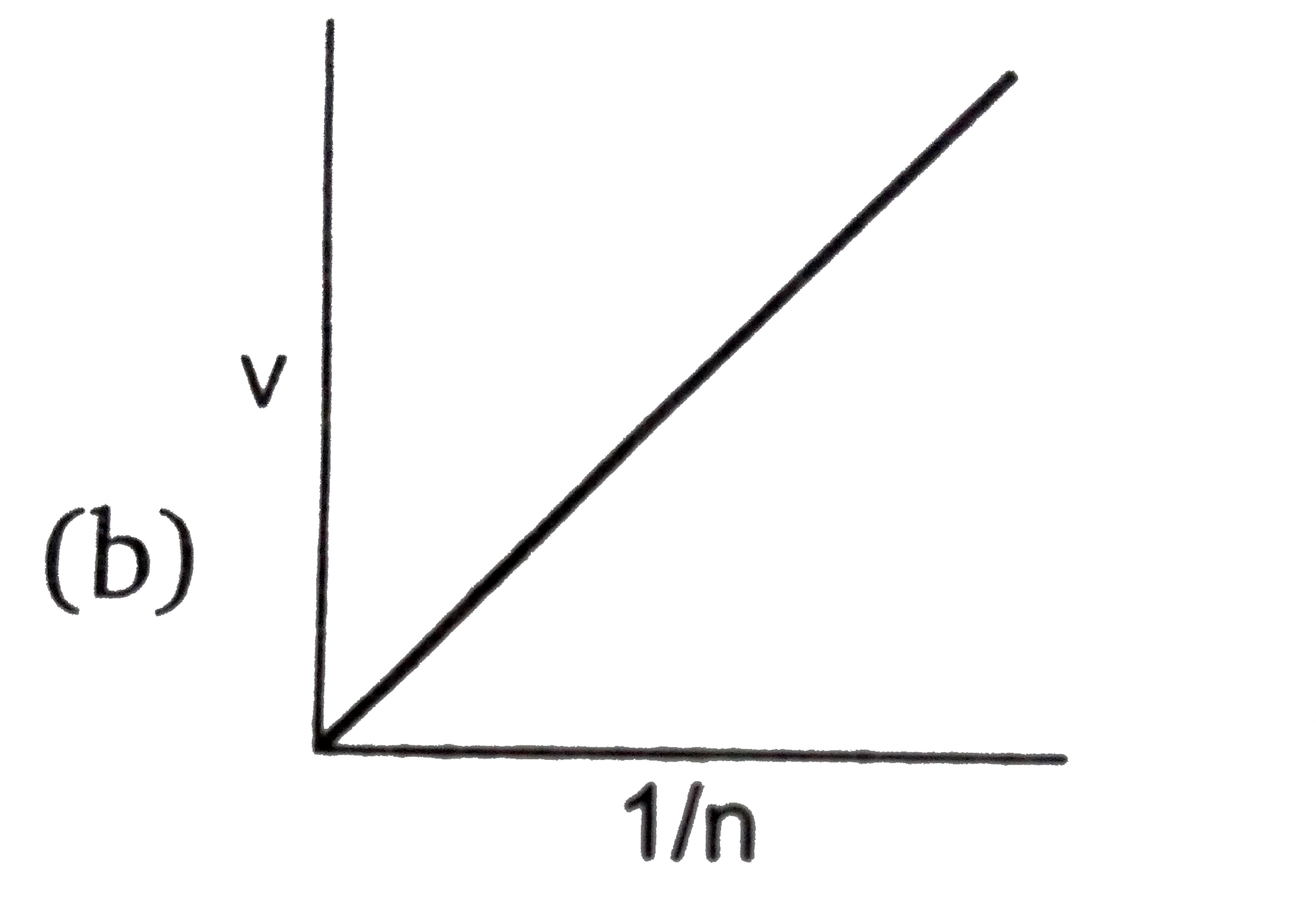

C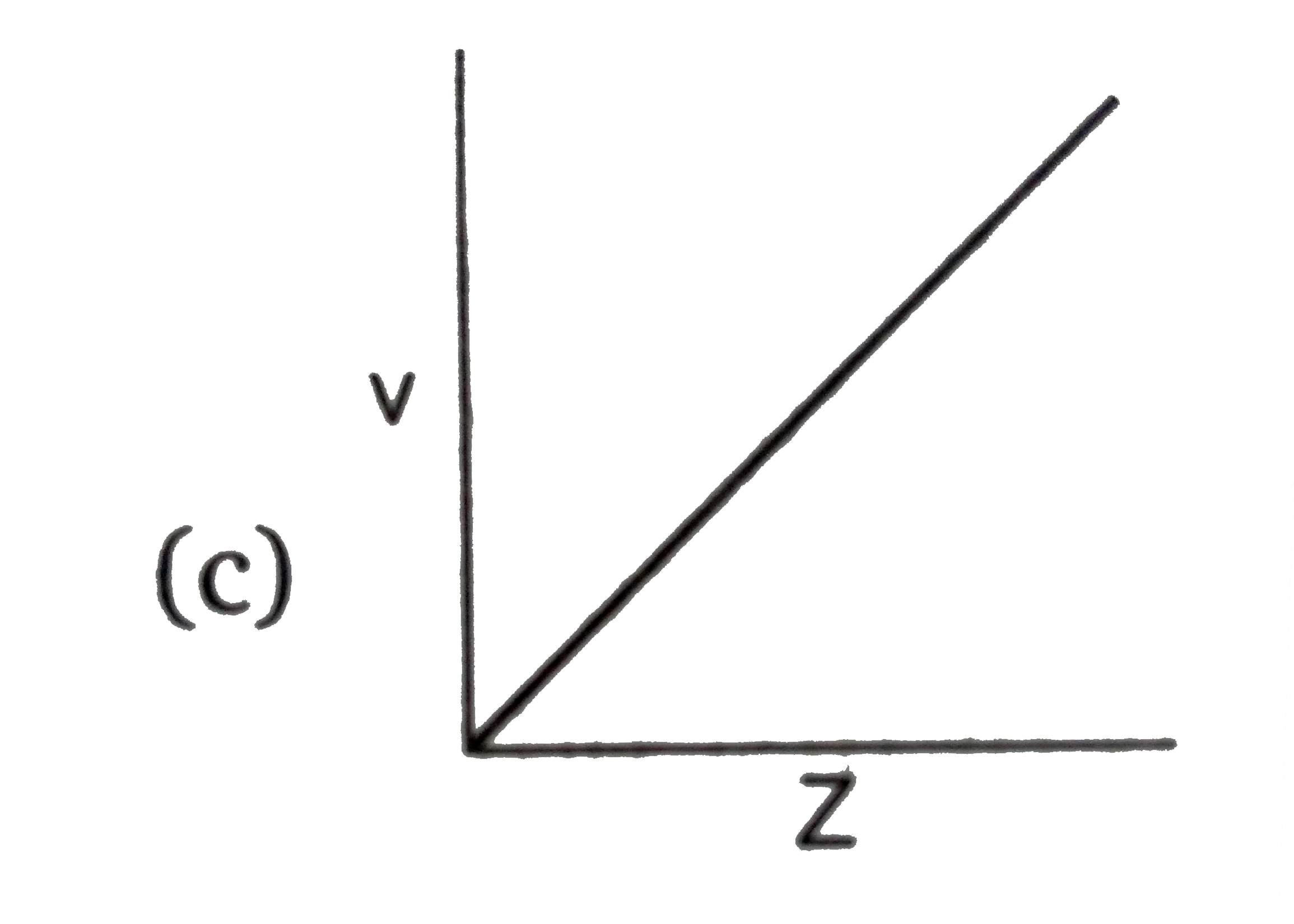

D

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem of selecting the incorrect graph for the velocity of an electron in an orbit versus Z, \( \frac{1}{n} \), and \( n \), we can follow these steps:
### Step-by-Step Solution:
1. **Understand the relationship between velocity, Z, and n**:
The velocity \( v \) of an electron in an orbit is derived from the balance of forces acting on it. The centrifugal force is equal to the electrostatic force. This can be expressed as:
\[
mv^2/r = \frac{kZe^2}{4\pi \epsilon_0 r^2}
\]
where \( m \) is the mass of the electron, \( v \) is its velocity, \( r \) is the radius of the orbit, \( Z \) is the atomic number, \( e \) is the charge of the electron, and \( k \) is Coulomb's constant.
2. **Use angular momentum quantization**:
The angular momentum of the electron is quantized:
\[
mvr = n\frac{h}{2\pi}
\]
where \( n \) is a principal quantum number and \( h \) is Planck's constant.
3. **Derive the formula for velocity**:
By substituting \( r \) from the angular momentum equation into the force balance equation, we can derive that:
\[
v = \frac{2\pi^2 k e^2 Z}{n h}
\]
This shows that the velocity \( v \) is proportional to \( \frac{Z}{n} \):
\[
v \propto \frac{Z}{n}
\]
4. **Analyze the graphs**:
- **Graph A (v vs n)**: Since \( v \) is inversely proportional to \( n \), this graph should be a rectangular hyperbola. This is correct.
- **Graph B (v vs \( \frac{1}{n} \))**: Since \( v \) is directly proportional to \( \frac{1}{n} \), this graph should be a straight line passing through the origin. This is correct.
- **Graph C (v vs Z)**: Since \( v \) is directly proportional to \( Z \), this graph should also be a straight line passing through the origin. This is correct.
- **Graph D (v vs n)**: This graph is claimed to be a straight line with a negative slope, which contradicts the derived relationship that \( v \) is inversely proportional to \( n \) (should be a rectangular hyperbola). This is incorrect.
5. **Conclusion**:
The incorrect graph is **Graph D**, which incorrectly represents the relationship between velocity and \( n \).
### Final Answer:
The incorrect graph is **D**.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
Select the incorrect statement for e-wastes
Which of the following option(s) is/are independent of both n and Z for H- like species? U_(n) = Potential energy of electron in n^(th) orbit KE_(n) = Kinetic energy of electron in n^(th) orbit l_(n) = Angular momentam of electoron in n^(th) orbit v_(n) = Velcity of electron in n^(th) orbit f_(n) = Frequency of electron in n^(th) orbit T_(n) = Time period of revolution of electron in n^(th) orbit
If, in a hydrogen atom, radius of nth Bohr orbit is r_(n) frequency of revolution of electron in nth orbit is f_(n) and area enclosed by the nth orbit is A_(n) , then which of the pollowing graphs are correct?
Calculate the velocity of the electron in the third orbit of hydrogen atom Hint : v= ( 2.18 xx 10^(6)z)/( n) m//s
Show the nature of the following graph for a satellite orbiting the earth. (a) K E vs orbitial radius R (b) PE vs orbital radius r (c ) TE vs orbital radius R .
Calculate the energy associated with the first orbit of He^(+) .What is the radius of this orbit ? Hint : E_(n) = - 2.18 xx10^(-18) ((Z^(2))/( n^(2))) J // atom He^(+) ( Z=2) r_(n) = ( 52.9(n^(2)))/(Z) pm
n, l and m values of the 2p_(z) orbital are
If the magnitude of energy of the electron in nth Bohr orbit is E_n and J_n is its angular momentum , then
In the Bohr's model , for unielectronic species following symbols are used r_(n,z)to Radius of n^"th" orbit with atomic number "z" U_(n,z)to Potential energy of electron in n^"th" orbit with atomic number "z" K_(n,z)to Kinetic energy of electron in n^"th" orbit with atomic number "z" V_(n,z)to Velocity of electon in n^"th" orbit with atomic number "z" T_(n,z)to Time period of revolution of electon in n^"th" orbit with atomic number "z" Calculate z in all in cases. (i) U_(1,2):K_(1,z)=-8:9 (ii) r_(1,z):r_(2,1) =1:12 (iii) v_(1,z):v_(3,1)=15:1 (iv) T_(1,2):T_(2,z)=9:32 Report your answer as (2r-p-q-s) where p,q,r and s represents the value of "z" in parts (i),(ii),(iii),(iv).
The velocity of electron in a certain bohr orbit bears the ration 1.275 to the velocity of light a. What is the quentum (n) of orbit ? b. Calculate the wave number of radiation emitted when the electron jumps from (n + 1) state to the ground state (R) = 1.0987 xx 10^(5) cm^(-1)