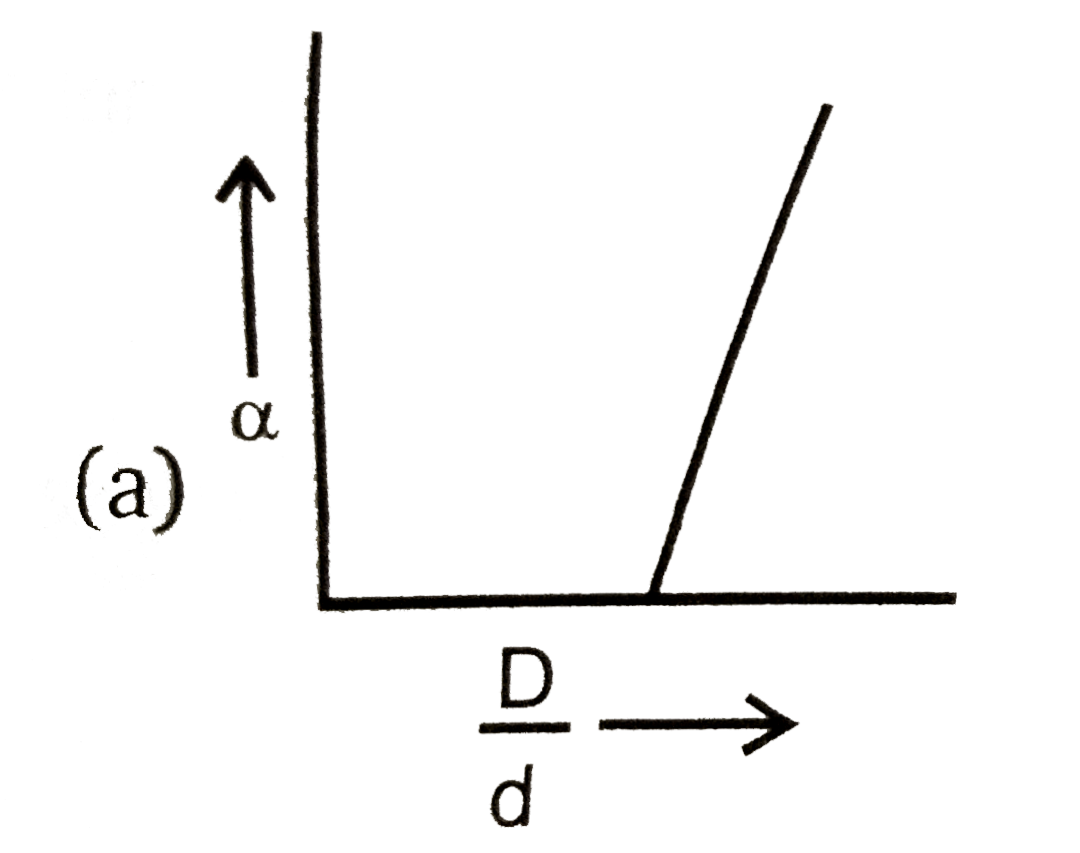
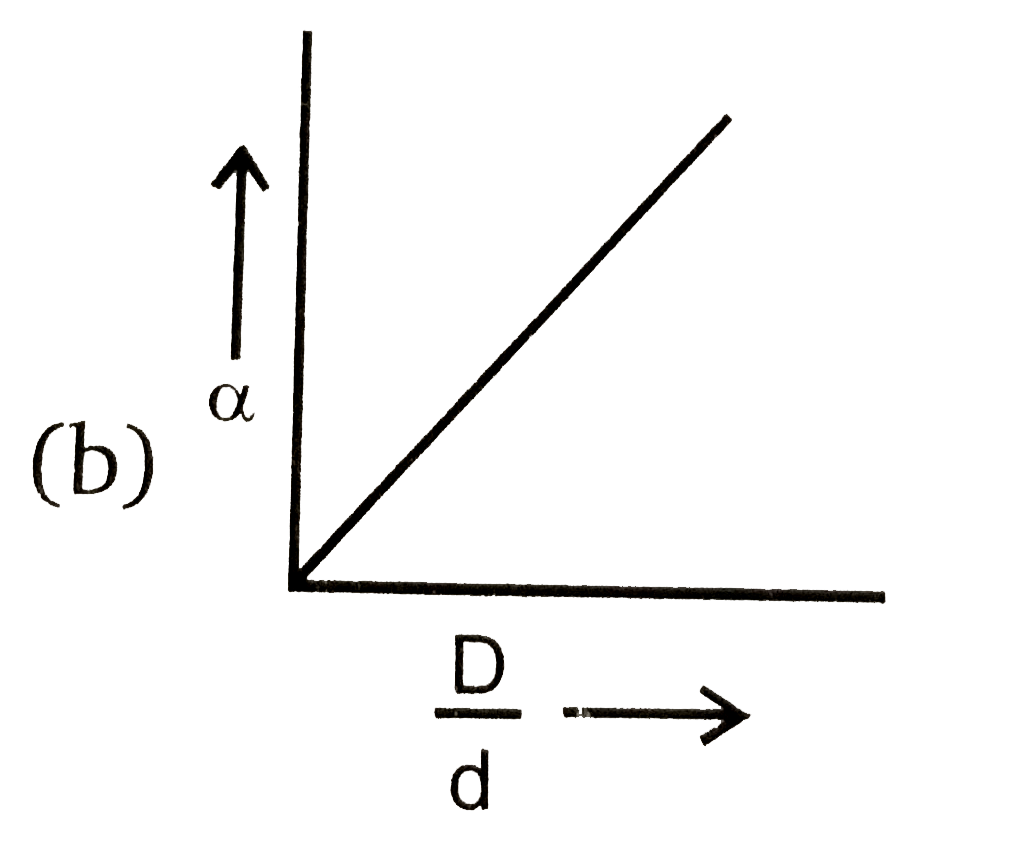
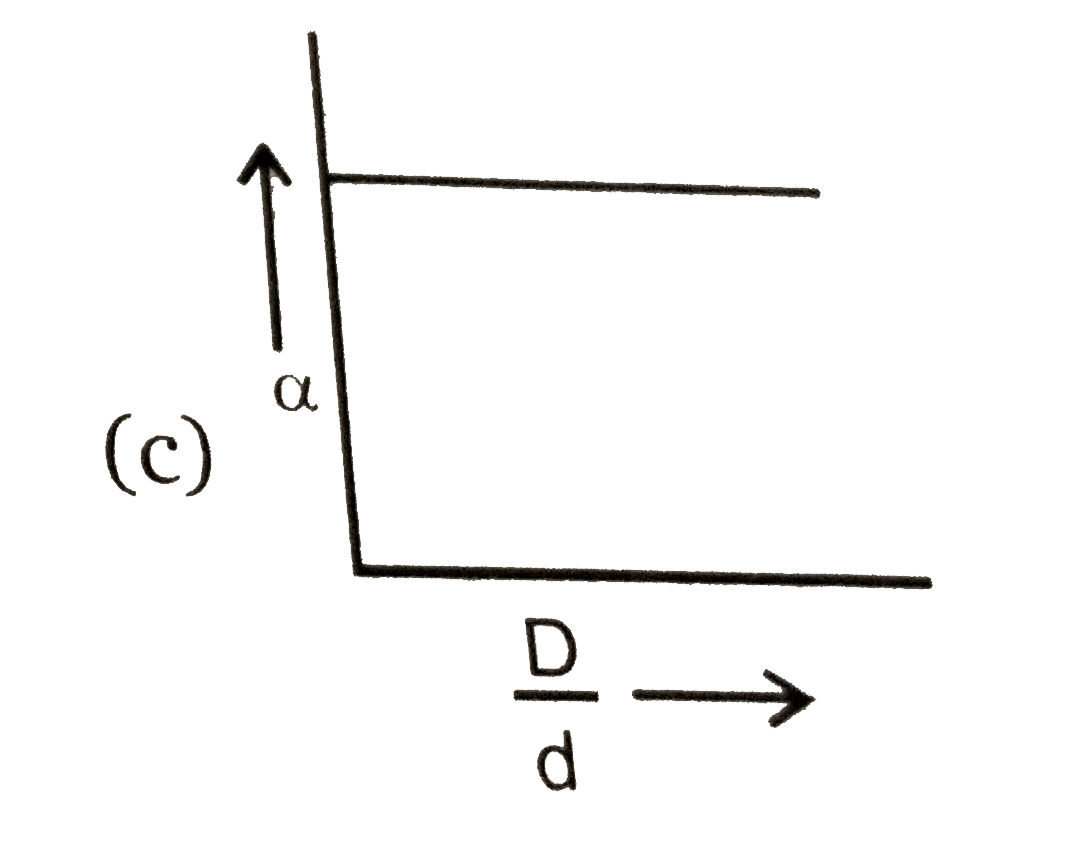
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- For the dissociation of PCl(5) into PCl(3) and Cl(2) in gaseous phase ...
Text Solution
|
- The equation alpha=(D-d)/((n-1)d) is correctly matched for: ( alpha is...
Text Solution
|
- For the dissociation of PCl(5) into PCl(3) and Cl(2) in gaseous phase ...
Text Solution
|
- In the dissociation of N(2)O(4) into NO(2), (1+ alpha) values with the...
Text Solution
|
- In the dissociation of N(2)O(4) into NO(2)O(4) into NO(2), alpha varie...
Text Solution
|
- For a very small extent of dissociation of PCl(5) into PCl(3) and Cl(2...
Text Solution
|
- For the dissociation of NH(3)(g) as 2NH(3)(g)iffN(2)(g)+3H(2)(g) , the...
Text Solution
|
- Consider the following hypothetical equilibrium 2B(g)hArrB(2)(g) I...
Text Solution
|
- The Vapour Density of mixture of PCl(5), PCl(3) and Cl(2) is 92. Find ...
Text Solution
|