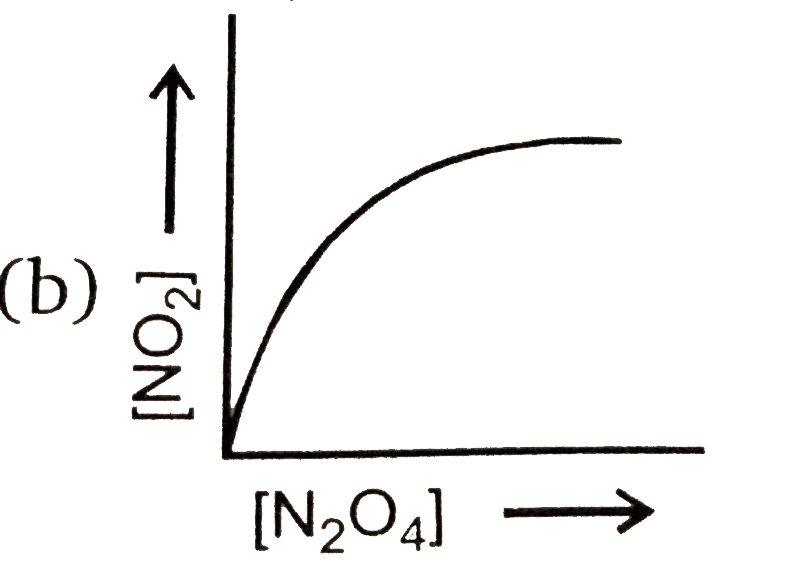
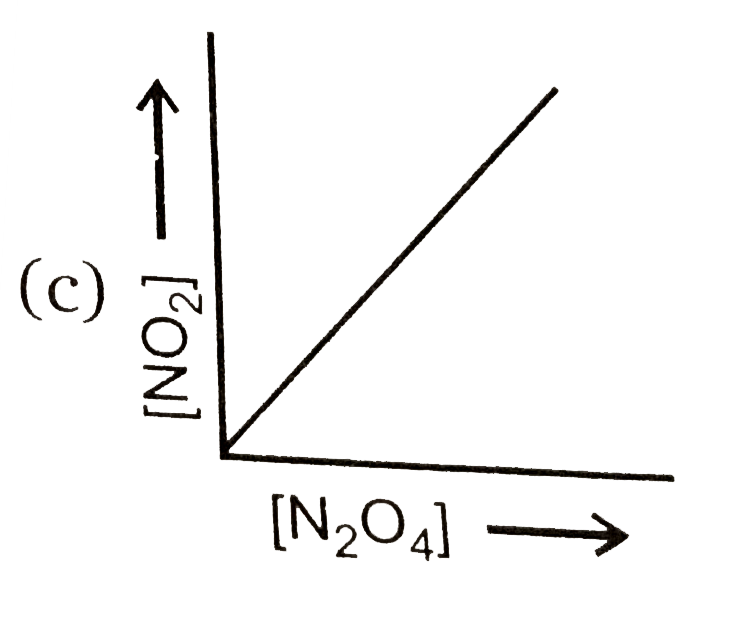
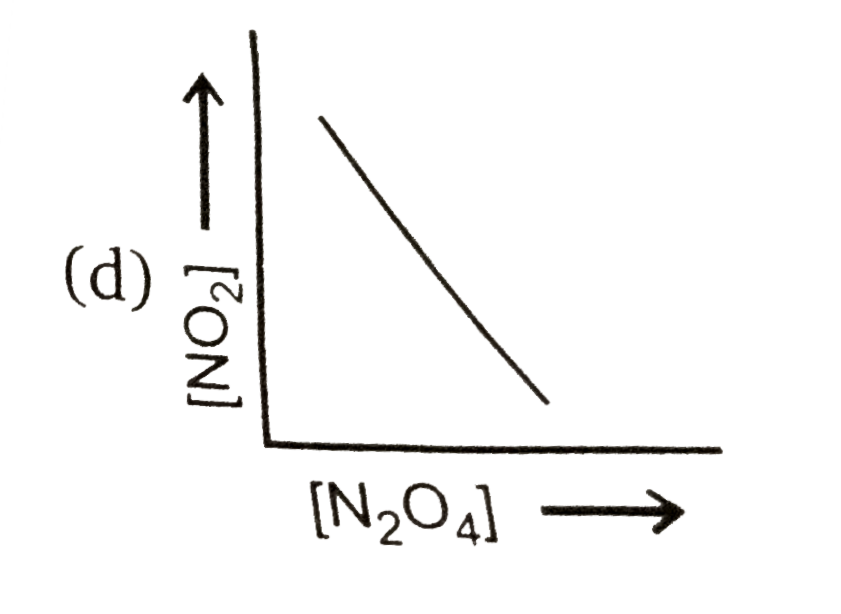
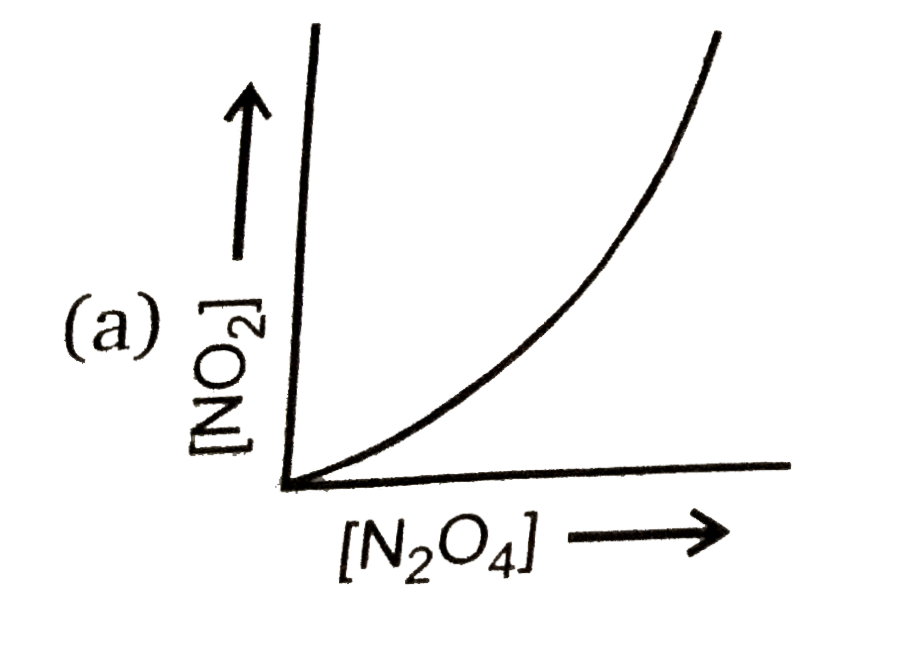A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider the following equilibrium N(2)O(4)(g)hArr2NO(2)(g) Then ...
Text Solution
|
- N(2)O(4) dissociates as N(2)O(4)(g)hArr2NO(2)(g) At 40^(@)C and on...
Text Solution
|
- Density of equilibrium mixture of N(2)O(4) and NO(2) at 1 atm and 384 ...
Text Solution
|
- K(c) for N(2)O(4)(g) hArr 2NO(2)(g) is 0.00466 at 298 K. If a 1-L cont...
Text Solution
|
- For the reaction at 25^(@)C , N(2)O(4(g))hArr2NO(2(g)) , if DeltaG(f)^...
Text Solution
|
- If the equilibrium constant for the reaction, N(2)O(4)hArr2NO(2) is K=...
Text Solution
|
- For the reaction equilibrium, N(2)O(4(g))hArr2NO(2(g)), the concentrat...
Text Solution
|
- Consider the following equilibrium N(2)O(4)(g)hArr2NO(2)(g) Then ...
Text Solution
|
- Vapour density of the equilibrium mixture of NO(2) "and" N(2)O(4) is f...
Text Solution
|