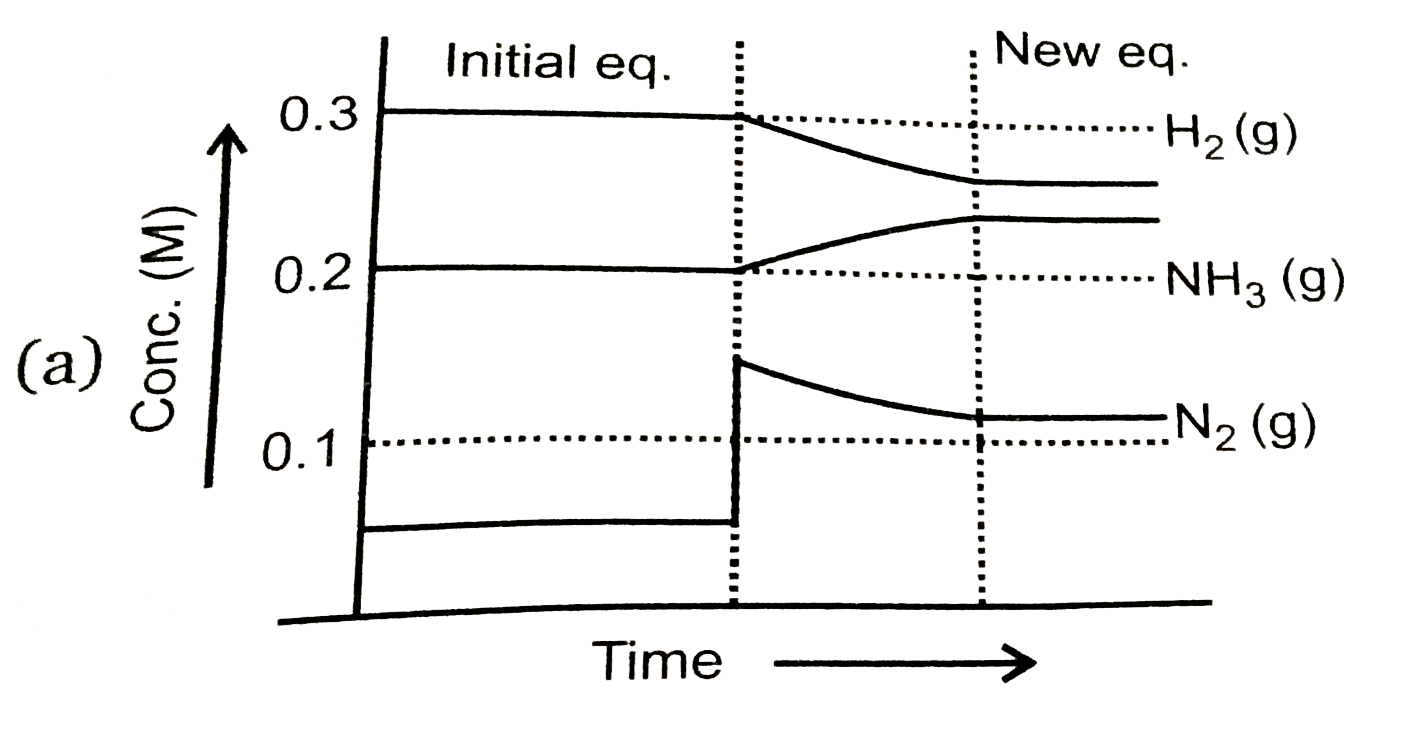
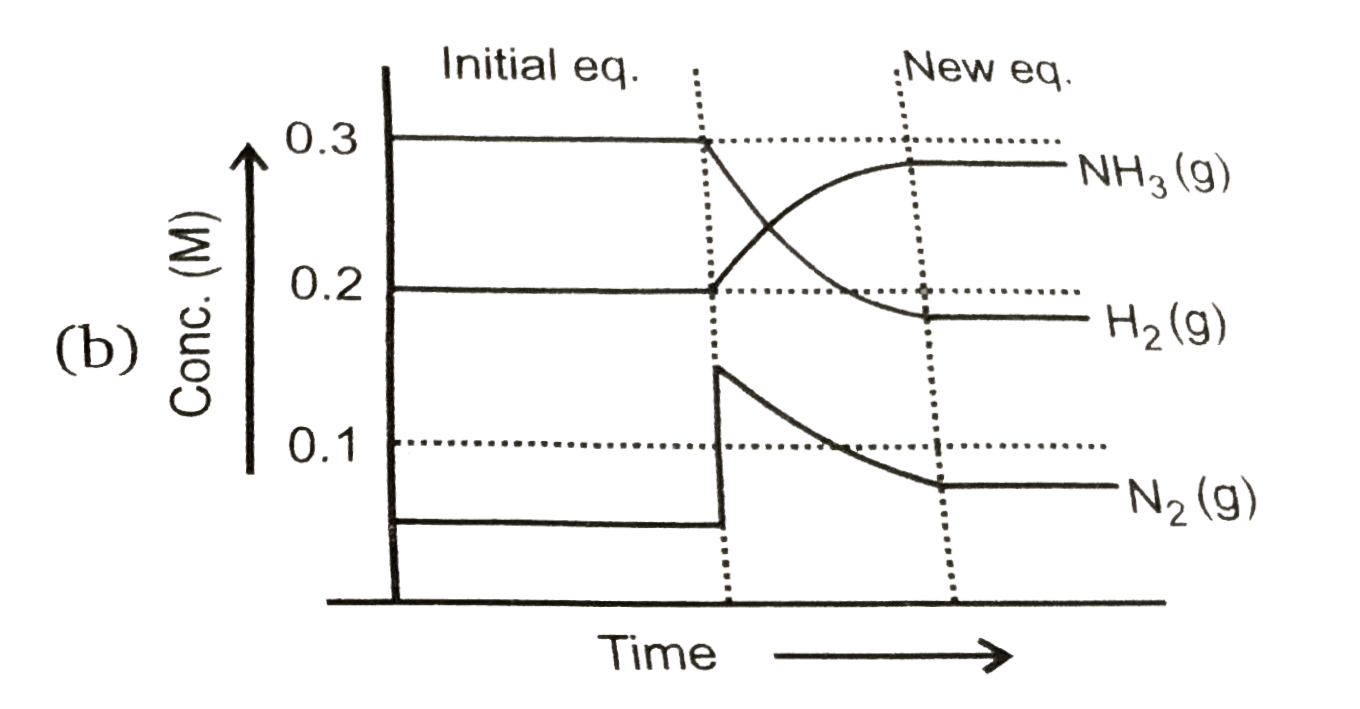
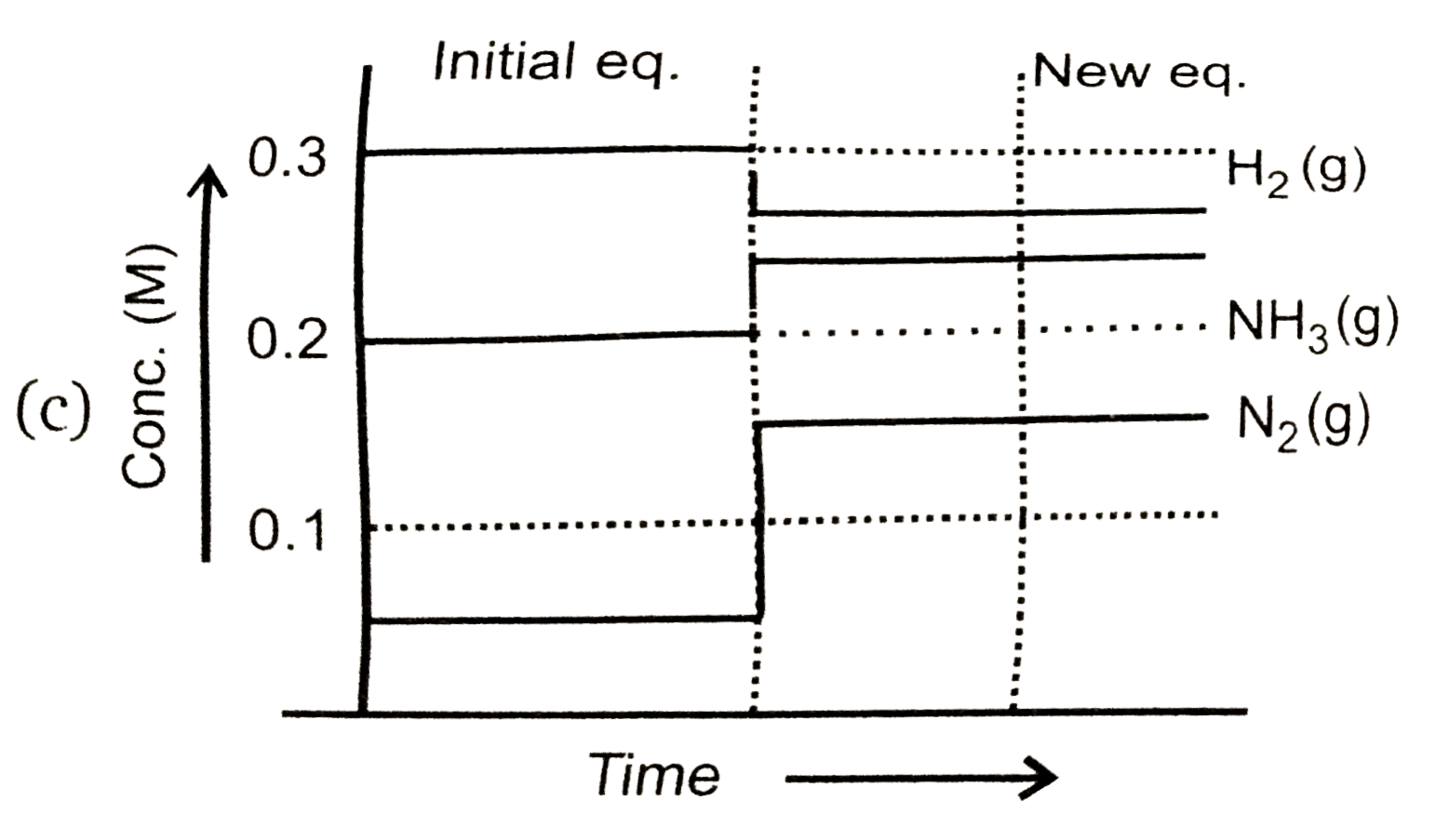
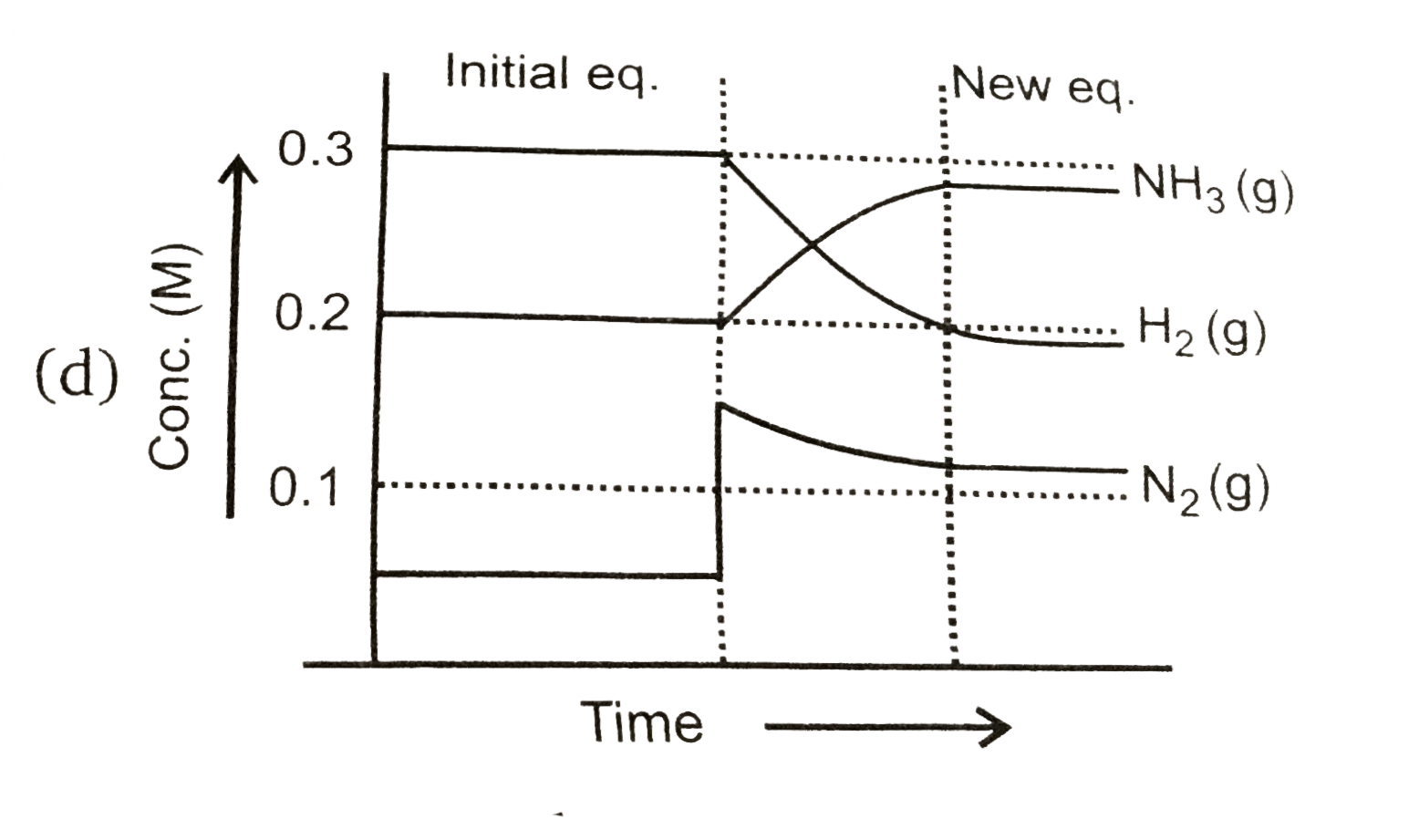
To solve the problem, we need to analyze the equilibrium reaction and the changes that occur when we add \( N_2(g) \) to the system.
### Step-by-Step Solution:
1. **Identify the Initial Conditions**:
- The initial concentrations before adding \( N_2(g) \) are:
- \( [N_2] = 0.05 \, M \)
- \( [NH_3] = 0.2 \, M \)
2. **Disturb the Equilibrium**:
- After adding \( N_2(g) \), the concentration becomes \( [N_2] = 0.15 \, M \).
3. **Determine the Change in Concentration**:
- The change in concentration of \( N_2 \) is:
\[
\Delta [N_2] = 0.15 \, M - 0.05 \, M = 0.10 \, M
\]
4. **Apply Le Chatelier's Principle**:
- According to Le Chatelier's principle, if we increase the concentration of a reactant, the system will shift to the right to counteract the change, thereby producing more products.
5. **Stoichiometry of the Reaction**:
- The balanced reaction for the formation of ammonia from nitrogen and hydrogen is:
\[
N_2(g) + 3H_2(g) \rightleftharpoons 2NH_3(g)
\]
- From the stoichiometry of the reaction:
- For every 1 mole of \( N_2 \) that reacts, 3 moles of \( H_2 \) are consumed and 2 moles of \( NH_3 \) are produced.
6. **Calculate Changes in Concentration**:
- Since \( N_2 \) increases by \( 0.10 \, M \):
- The decrease in \( H_2 \) will be \( 3 \times 0.10 \, M = 0.30 \, M \).
- The increase in \( NH_3 \) will be \( 2 \times 0.10 \, M = 0.20 \, M \).
7. **Final Concentrations**:
- After the changes, the new concentrations will be:
- \( [N_2] = 0.15 \, M \)
- \( [H_2] = 0.2 \, M - 0.30 \, M = -0.10 \, M \) (impossible, indicating that the reaction will not proceed further)
- \( [NH_3] = 0.2 \, M + 0.20 \, M = 0.4 \, M \)
8. **Graph Representation**:
- The graph that represents this situation will show a decrease in \( H_2 \) concentration, an increase in \( NH_3 \) concentration, and a slight change in \( N_2 \) concentration.
### Conclusion:
The correct graph that represents the changes in concentrations of \( N_2 \), \( H_2 \), and \( NH_3 \) after the addition of \( N_2(g) \) is option D, as it matches the stoichiometric changes predicted by the equilibrium shift.