Home
Class 12
MATHS
The equation of the circle passing th...

The equation of the circle passing through the foci of the ellipse `(x^2)/(16)+(y^2)/9=1` , and having centre at (0, 3) is (1) `x^2+y^2-6y+7=0` (2) `x^2+y^2-6y-5=0` (3) `x^2+y^2-6y+5=0` (4) `x^2+y^2-6y-7=0`

Text Solution

Verified by Experts

Coordinates for focia re (ae, 0) , (-ar, 0)
`:. e=sqrt(1-(9)/(16))rArre=(sqrt(7))/(4)`
Coordinates of foci are `(sqrt(7),0),(-sqrt(7),0)`

Radius ` R=sqrt(7+9)=4`
Promotional Banner

Topper's Solved these Questions

  • DIFFERENTIAL EQUATIONS

    JEE MAINS PREVIOUS YEAR ENGLISH|Exercise All Questions|10 Videos

  • HYPERBOLA

    JEE MAINS PREVIOUS YEAR ENGLISH|Exercise All Questions|2 Videos

Similar Questions

Explore conceptually related problems

The equation of the circle passing through the point of intersection of the circle x^2+y^2=4 and the line 2x+y=1 and having minimum possible radius is (a) 5x^2+5y^2+18 x+6y-5=0 (b) 5x^2+5y^2+9x+8y-15=0 (c) 5x^2+5y^2+4x+9y-5=0 (c) 5x^2+5y^2-4x-2y-18=0

Equation of circle passing through the centre of the circle x^2+y^2-4x-6y-8=0 and being concentric with the circle x^2+y^2-2x-8y-5=0 is

The equation of the circle concentric to the circle 2x^(2)+2y^(2)-3x+6y+2=0 and having double the area of this circle, is

The equation of the circle passing through (1,2) and the points of intersection of the circles x^2+y^2-8x-6y+21=0 and x^2+y^2-2x-15=0 is

The equation of the circle having the intercept on the line y+2x=0 by the circle x^2 + y^2 + 4x + 6y = 0 as a diameter is : (A) 5x^2 + 5y^2 - 8x + 16y =0 (B) 5x^2 + 5y^2 + 8x - 16y =0 (C) 5x^2 + 5y^2 - 8x - 16y =0 (D) 5x^2 + 5y^2 + 8x+- 16y =0

The equation of the circle passing through the point of intersection of the circles x^2 + y^2 - 6x + 2y + 4 = 0 and x^2 + y^2 + 2x - 6y - 6=0 and having its centre on y=0 is : (A) 2x^2 + 2y^2 + 8x + 3 = 0 (B) 2x^2 + 2y^2 - 8x - 3 = 0 (C) 2x^2 + 2y^2 - 8x + 3 = 0 (D) none of these

Find the equation of the circle concentric with the circle x^2 +y^2 - 4x - 6y-9=0 and passing through the point (-4, -5)

The equation of the circle having its centre on the line x+2y-3=0 and passing through the points of intersection of the circles x^2+y^2-2x-4y+1=0a n dx^2+y^2-4x-2y+4=0 is x^2+y^2-6x+7=0 x^2+y^2-3y+4=0 c. x^2+y^2-2x-2y+1=0 x^2+y^2+2x-4y+4=0

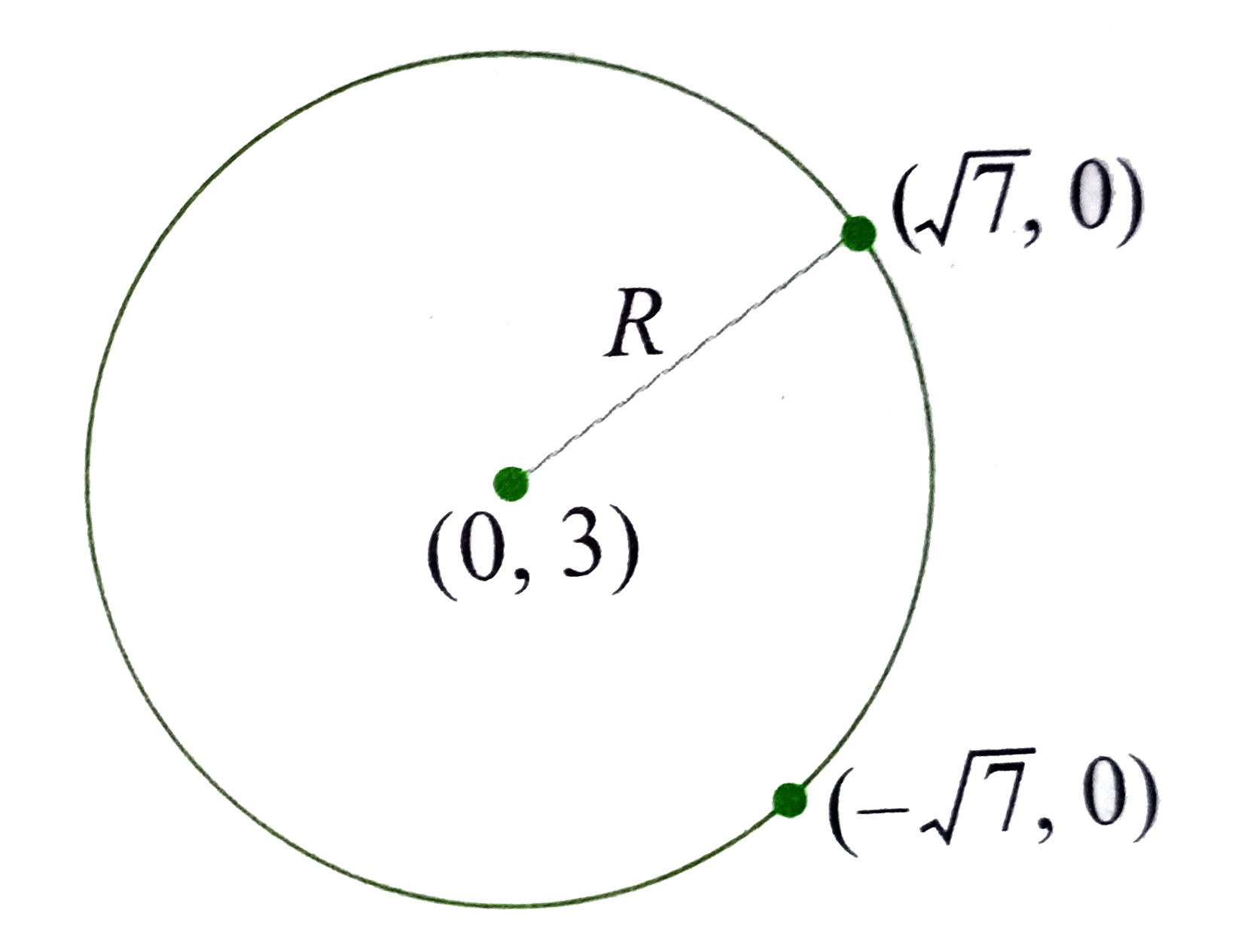
Find the equation of the circle concentric with the circle x^(2) + y^(2) - 8x + 6y -5 = 0 and passing through the point (-2, -7).

Find the equation of circle passing through the origin and cutting the circles x^(2) + y^(2) -4x + 6y + 10 =0 and x^(2) + y^(2) + 12y + 6 =0 orthogonally.