Two identical beakers `A` and `B` contain equal volumes of two different liquids at `60^(@)C` each and left to cool down. Liquid in A has density of `8xx10^(2)kg//m^(2)` and specific heat of `2000J kg^(-1)K^(-1)` while liquid in `B` has density of `10^(3)kg m^(-3)` and specific heat of `400J kg^(-1)K^(-1)`. Which of the following best describes their temperature versus time graph schematically? (assume the emissivity of both the beakers to be the same)
Two identical beakers `A` and `B` contain equal volumes of two different liquids at `60^(@)C` each and left to cool down. Liquid in A has density of `8xx10^(2)kg//m^(2)` and specific heat of `2000J kg^(-1)K^(-1)` while liquid in `B` has density of `10^(3)kg m^(-3)` and specific heat of `400J kg^(-1)K^(-1)`. Which of the following best describes their temperature versus time graph schematically? (assume the emissivity of both the beakers to be the same)
A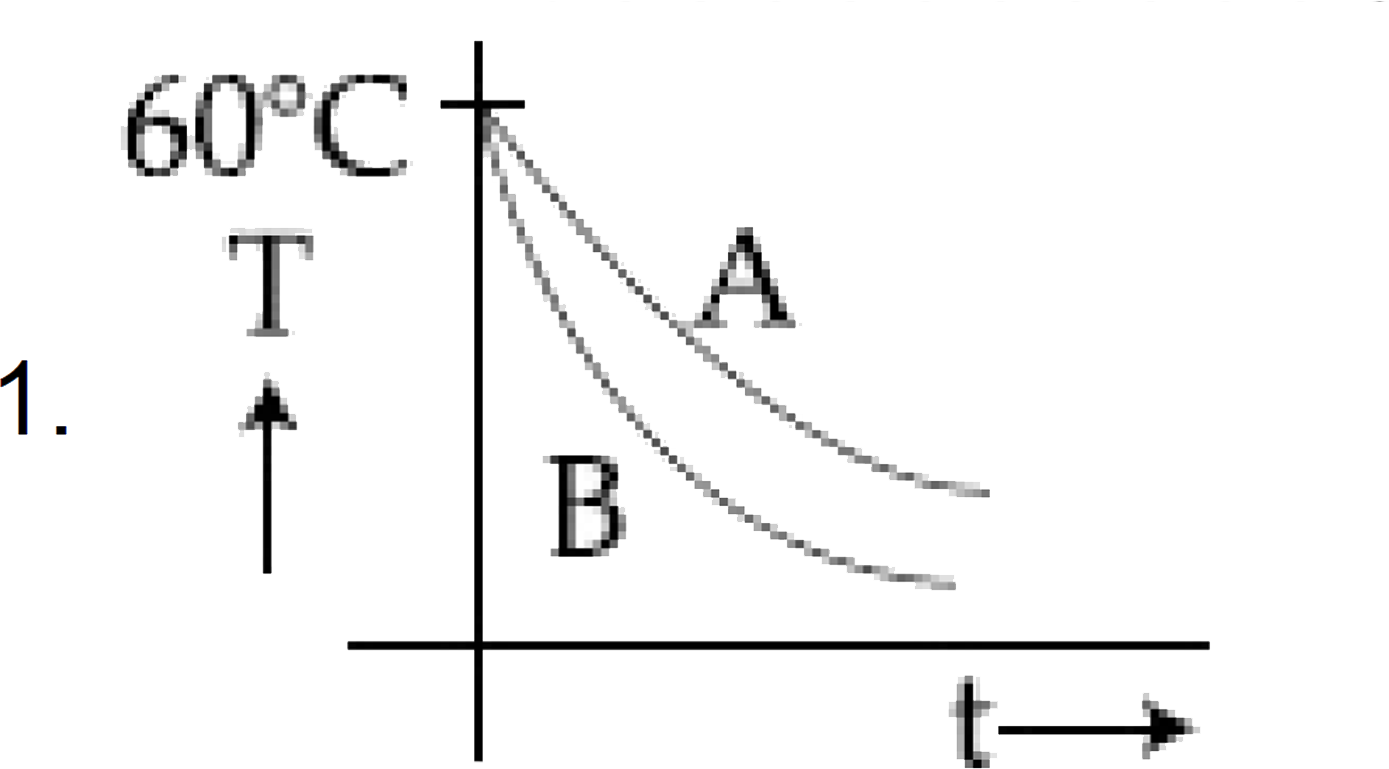

B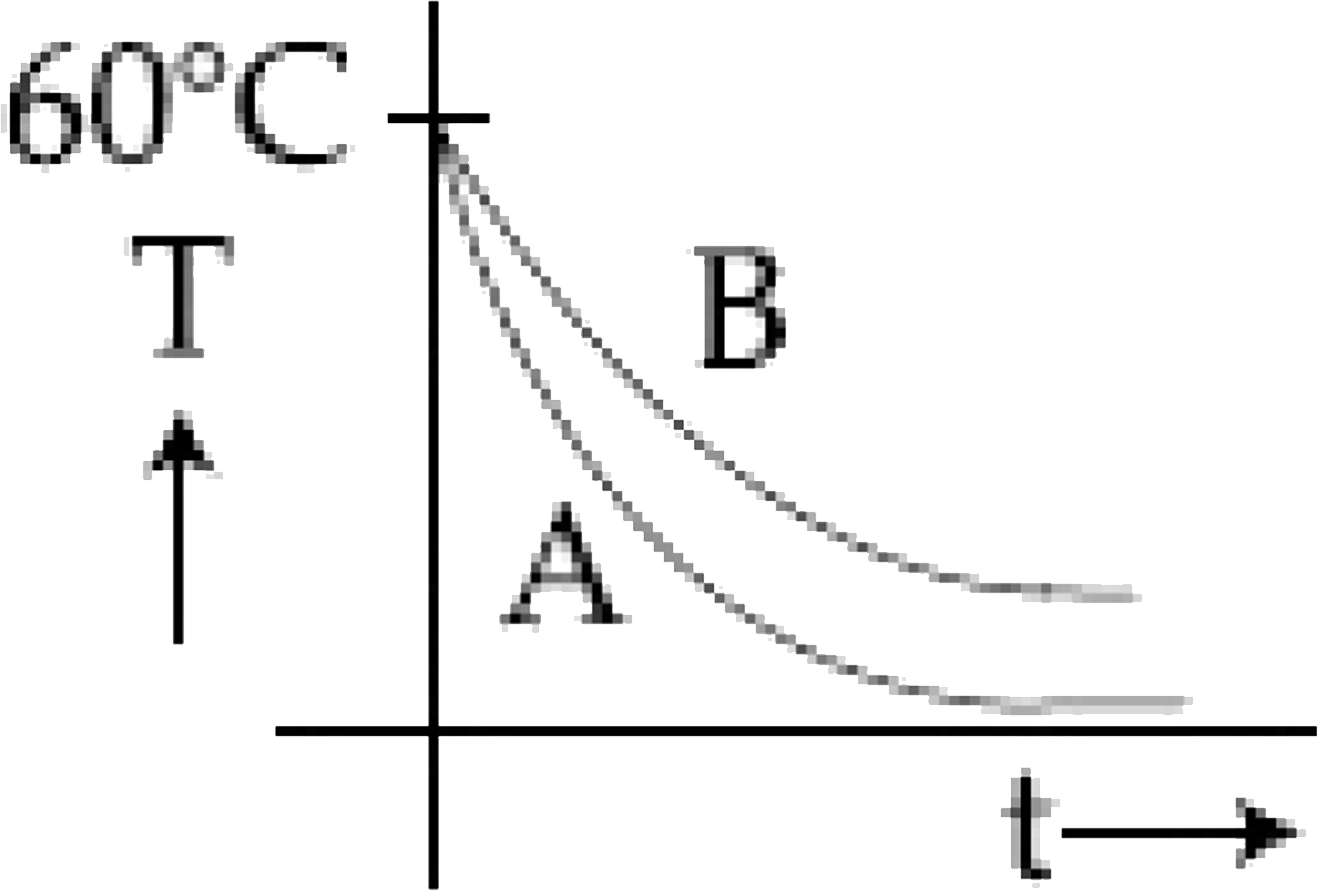

C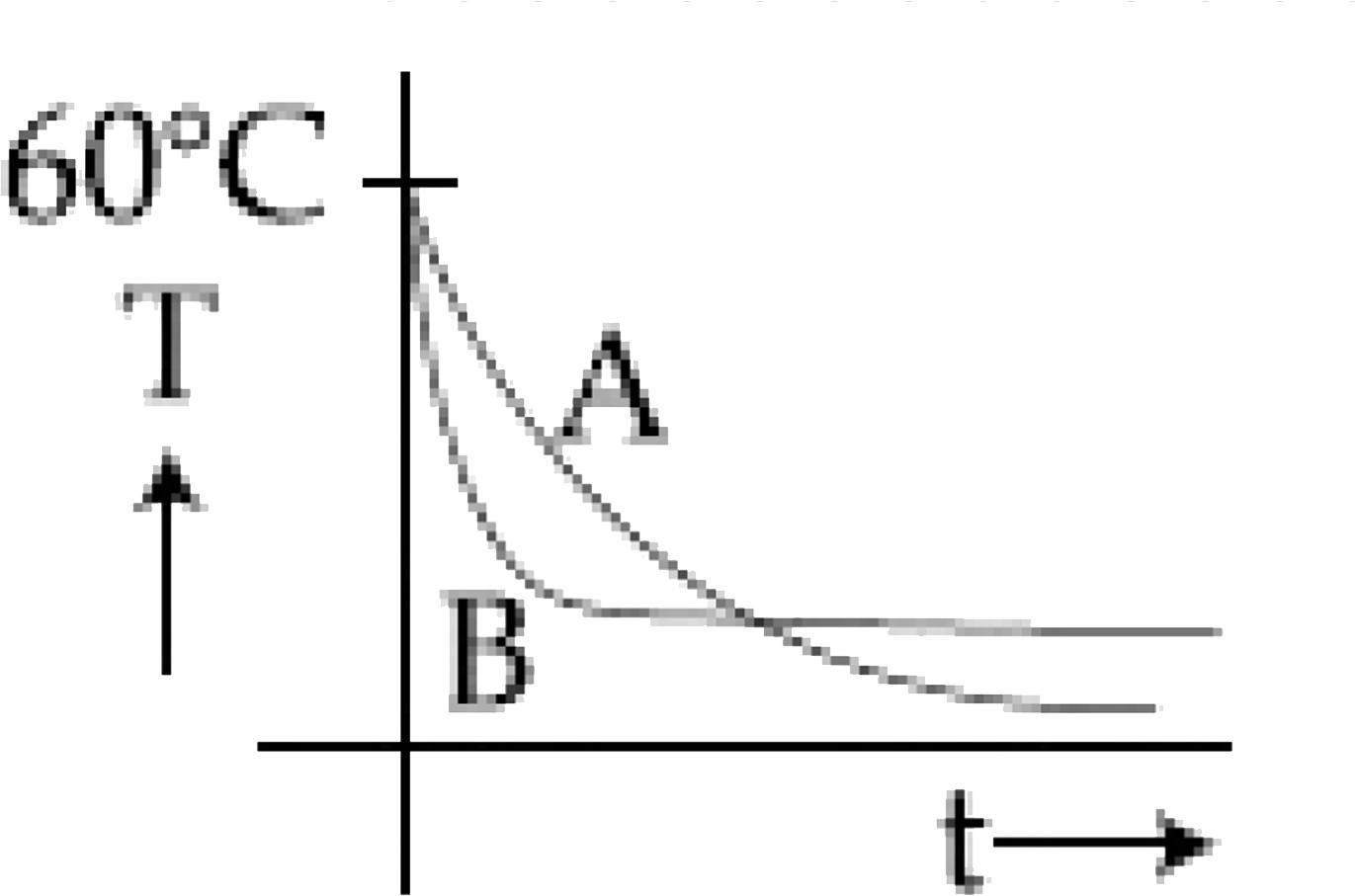

D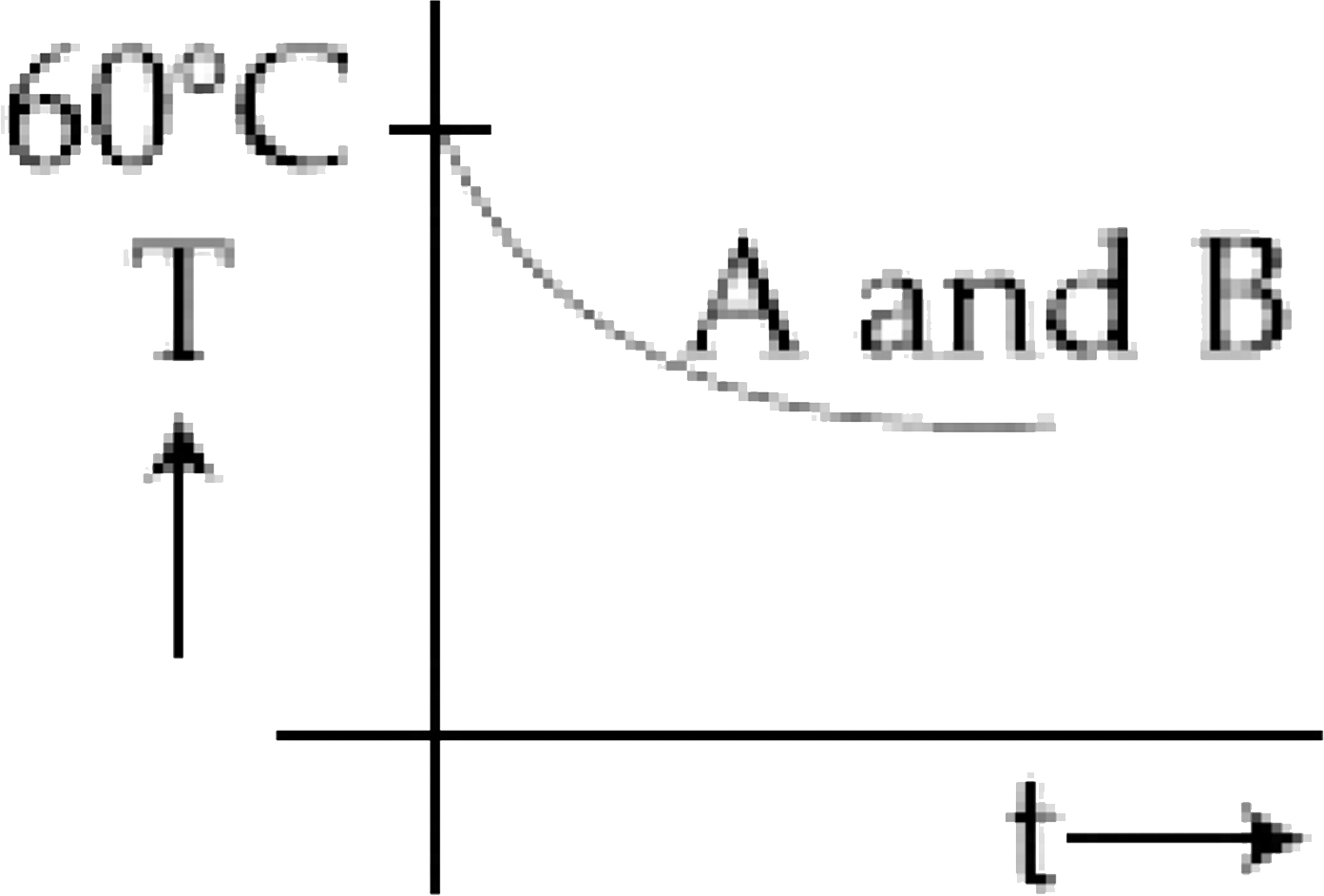
Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem, we need to analyze the cooling rates of the two liquids in beakers A and B based on their mass and specific heat capacities. We will use Newton's law of cooling to derive the temperature versus time graph.
### Step-by-Step Solution:
1. **Identify the Given Data:**
- Beaker A:
- Density, \( \rho_A = 8 \times 10^2 \, \text{kg/m}^3 \)
- Specific heat, \( c_A = 2000 \, \text{J/(kg K)} \)
- Beaker B:
- Density, \( \rho_B = 10^3 \, \text{kg/m}^3 \)
- Specific heat, \( c_B = 400 \, \text{J/(kg K)} \)
- Both liquids start at \( T_0 = 60^\circ C \).
2. **Calculate the Mass of Liquids:**
- Let the volume of each liquid be \( V \).
- Mass of liquid in beaker A:
\[
m_A = \rho_A \cdot V = (8 \times 10^2) \cdot V = 800V \, \text{kg}
\]
- Mass of liquid in beaker B:
\[
m_B = \rho_B \cdot V = (10^3) \cdot V = 1000V \, \text{kg}
\]
3. **Calculate the Heat Capacity (m*c) for Each Liquid:**
- Heat capacity for liquid A:
\[
m_A \cdot c_A = (800V) \cdot (2000) = 1.6 \times 10^6 V \, \text{J/K}
\]
- Heat capacity for liquid B:
\[
m_B \cdot c_B = (1000V) \cdot (400) = 4.0 \times 10^5 V \, \text{J/K}
\]
4. **Determine the Cooling Rate Using Newton's Law of Cooling:**
- According to Newton's law of cooling, the rate of change of temperature is proportional to the temperature difference:
\[
\frac{dT}{dt} \propto (T - T_{\text{ambient}})
\]
- The proportionality constant is inversely related to the heat capacity:
\[
\frac{dT}{dt} = -k \cdot \frac{1}{m \cdot c} \cdot (T - T_{\text{ambient}})
\]
- Therefore, the cooling rate for each liquid can be expressed as:
\[
\frac{dT_A}{dt} = -k_A \cdot (T_A - T_{\text{ambient}}) \quad \text{and} \quad \frac{dT_B}{dt} = -k_B \cdot (T_B - T_{\text{ambient}})
\]
- Where \( k_A \) and \( k_B \) are constants depending on the heat capacity.
5. **Compare the Cooling Rates:**
- Since \( m_A \cdot c_A = 1.6 \times 10^6 V \) and \( m_B \cdot c_B = 4.0 \times 10^5 V \), we see that:
\[
m_A \cdot c_A > m_B \cdot c_B
\]
- This implies that the cooling rate for liquid A is slower than that for liquid B:
\[
\left| \frac{dT_A}{dt} \right| < \left| \frac{dT_B}{dt} \right|
\]
6. **Conclusion on Temperature vs. Time Graph:**
- Since liquid A cools more slowly than liquid B, the temperature vs. time graph will show that the temperature of liquid A decreases less steeply compared to liquid B.
- Thus, the graph for liquid A will be above that of liquid B for the same time interval.
### Final Answer:
The best schematic representation of the temperature versus time graph is option **B**, where the slope for liquid A is less than that for liquid B.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A sample of 10g H_(2)O is slowly heated from 27^(@)C to 87^(@)C . Calculate the change in entropy during heating. (specific heat of water =4200 J kg^(-1)K^(-1)) .
Find the result of mixing 0.5 kg ice at 0^@C with 2 kg water at 30^@C . Given that latent heat of ice is L=3.36xx10^5 J//kg and specific heat of water is 4200 J//kg//K .
Calculate the speed of longitudinal sound wave in a liquid. The bulk modulus for the liquid is 20xx10^(9)N//m^(2) and its density is 9.5xx10^(3)kg//m^(3) .
Calculate the difference in temperature between the water at the top and bottom of a water fall 200 m high. Specific heat capacity of water 42000 J kg ^(-1) K ^(-1).
Calculate the increase in the internal energy of 10 g of water when it is heated from 0^(0)C to 100^(0)C and converted into steam at 100 kPa. The density of steam =0.6 kg m^(-3) specific heat capacity of water =4200 J kg^(-1 ^(0)C^(-3) latent heat of vaporization of water =2.25xx10^(6) J kg^(-1)
A cubical tank of side 1 m is filled with 800 kg of a liquid. Find the density of liquid in kg m^(-3)
500 kg of water is heated from 20^(@) to 100^(@) C . Calculate the increase in the mass of water.Given specific heat of water =4.2 xx 10^(3) J kg ^(-1) .^(@)C^(-1) .
A liquid of mass m and specific heat c is heated to a temperature 2T. Another liquid of mass m/2 and specific heat 2 c is heated to a temperature T. If these two liquids are mixed, the resulting temperature of the mixture is
Write the expression for the heat energy Q received by m kg of a substance of specific heat capacity c J kg^(-1)K^(-1) when it is heated through Deltat^@ C.