A very long solenoid of radius R is carrying current `I(t)=kte^(-alphat)` , as a function of time `(tge0)`. Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :
A very long solenoid of radius R is carrying current `I(t)=kte^(-alphat)` , as a function of time `(tge0)`. Counter clockwise current is taken to be positive. A circular conducting coil of radius 2R is placed in the equatorial plane of the solenoid and concentric with the solenoid. the current induced inthe outer coil is correctly depicted, as function of time by :
A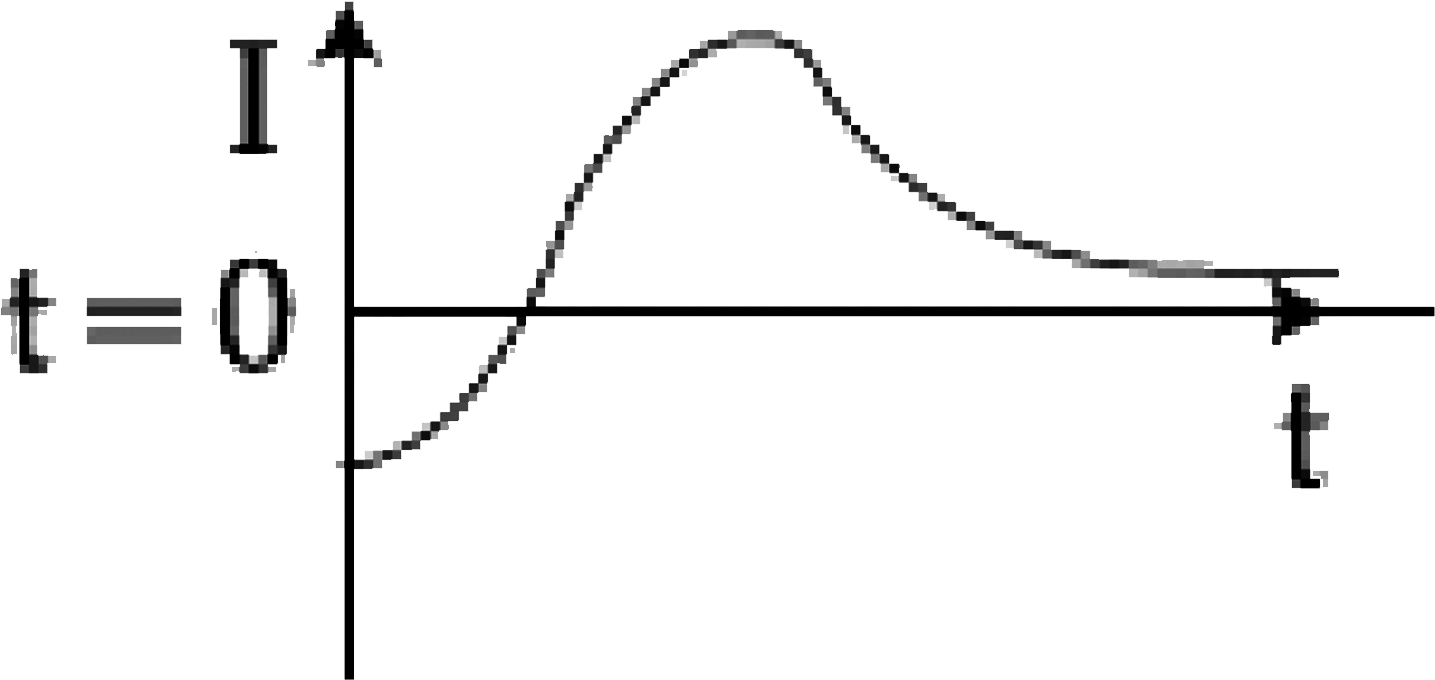

B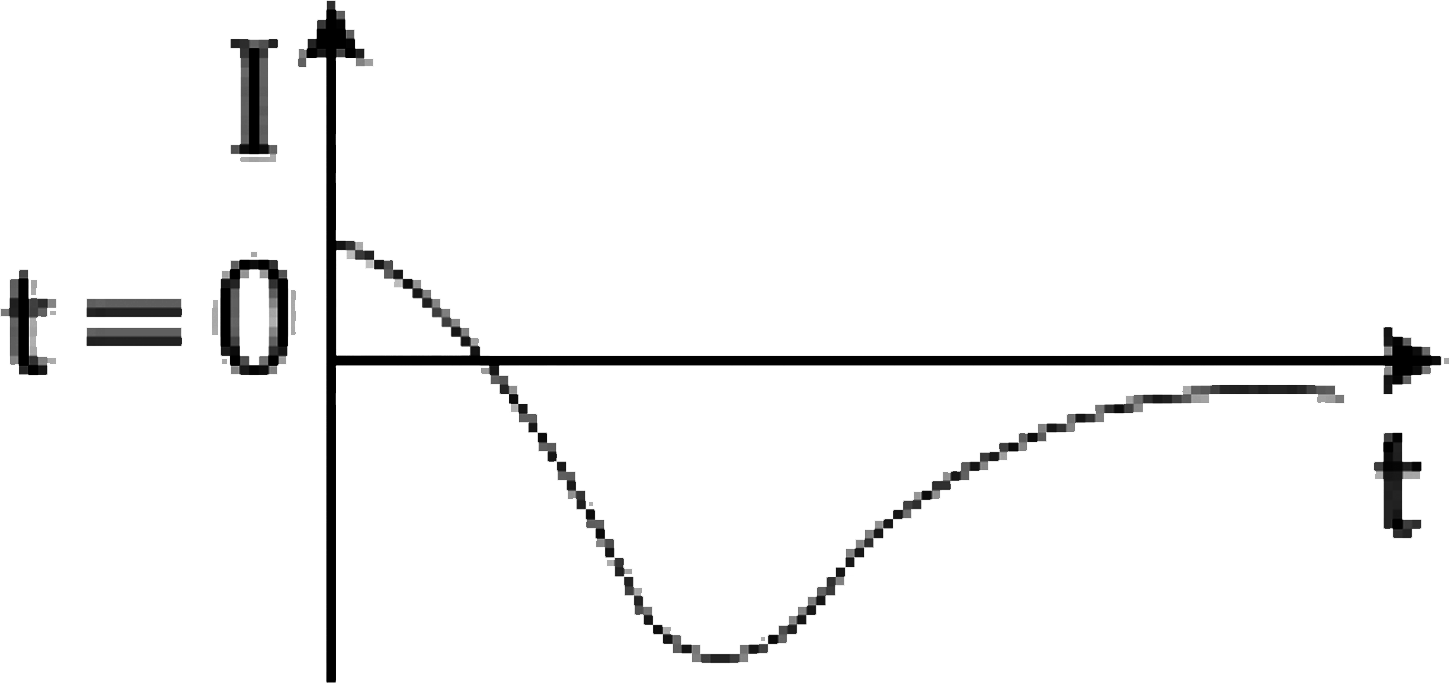

C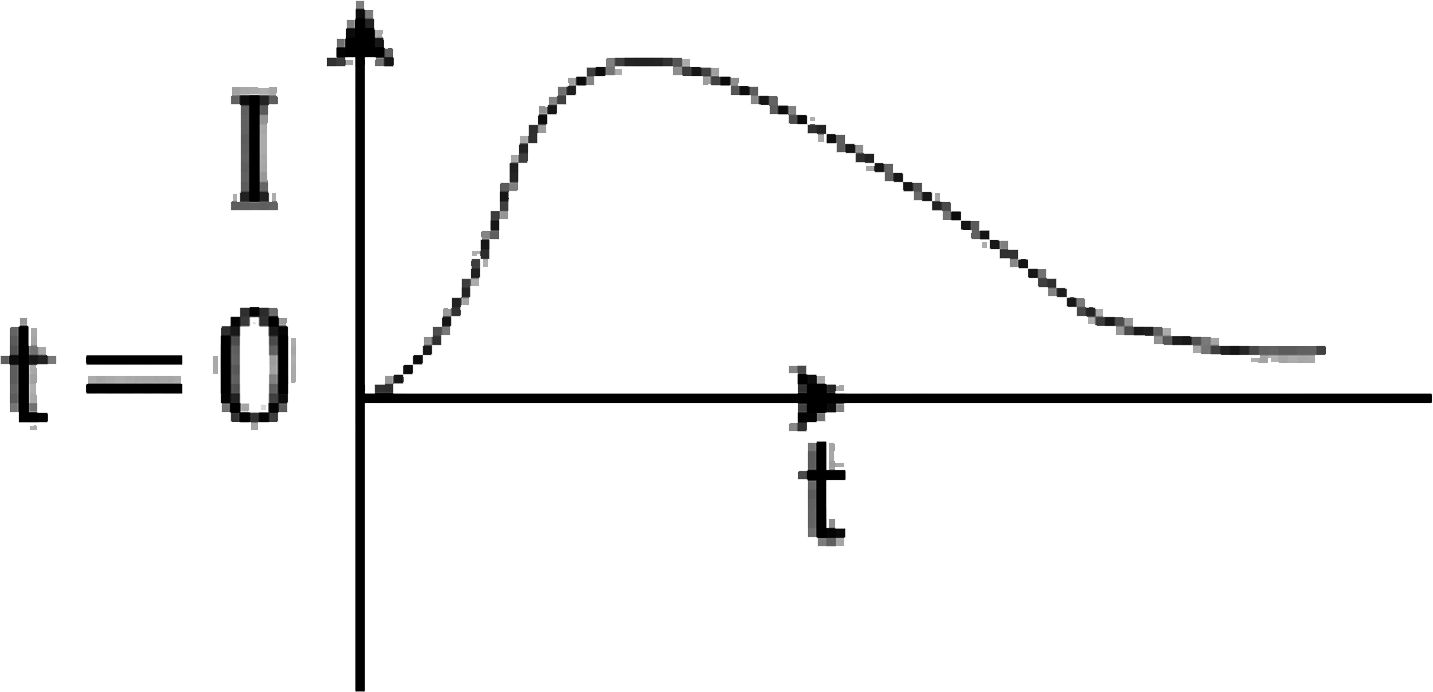

D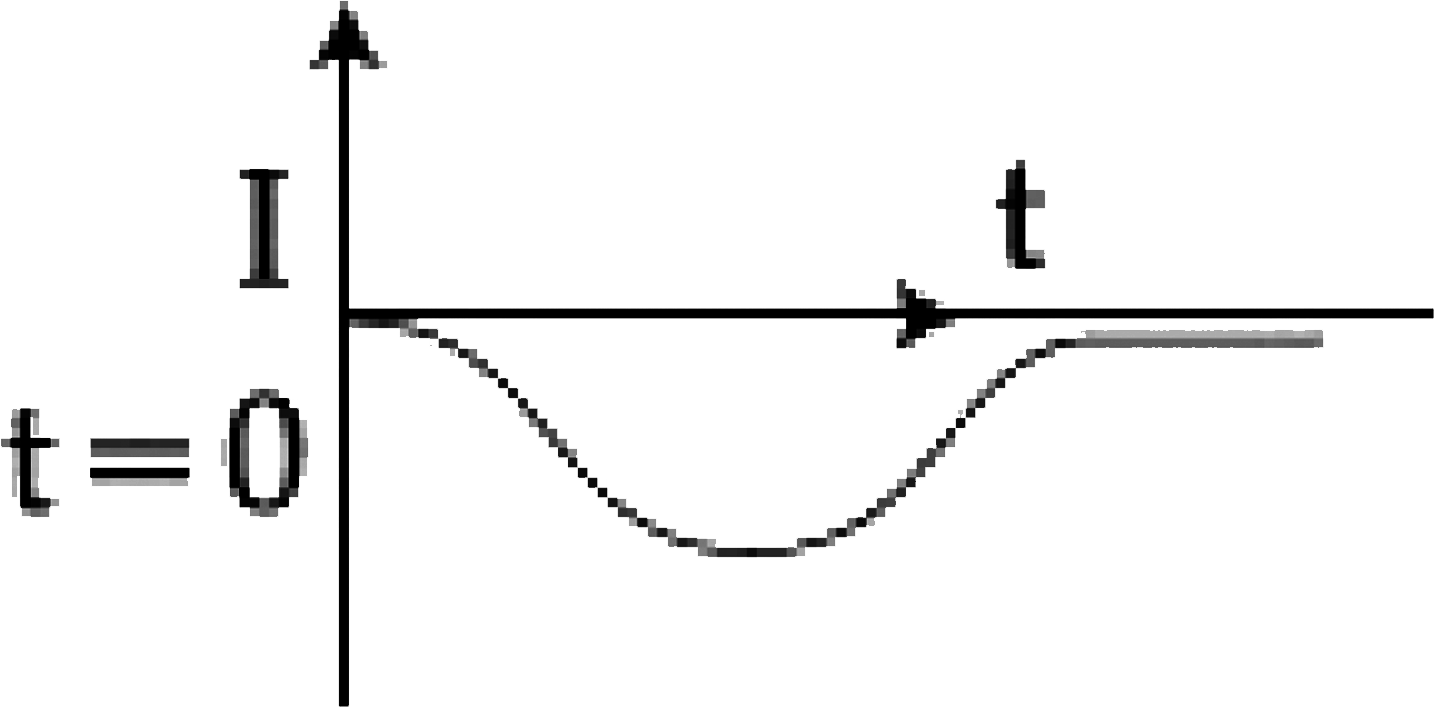

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem, we need to analyze the situation involving a long solenoid carrying a time-dependent current and the induced current in a concentric conducting coil placed in its equatorial plane.
### Step-by-Step Solution:
1. **Identify the Current in the Solenoid**:
The current in the solenoid is given by:
\[
I(t) = k t e^{-\alpha t}
\]
where \( k \) and \( \alpha \) are constants.
2. **Determine the Magnetic Field Inside the Solenoid**:
The magnetic field \( B \) inside a long solenoid carrying current \( I \) is given by:
\[
B = \mu_0 n I
\]
where \( \mu_0 \) is the permeability of free space and \( n \) is the number of turns per unit length. Since the solenoid is long and the current varies with time, we substitute \( I(t) \):
\[
B(t) = \mu_0 n (k t e^{-\alpha t})
\]
3. **Calculate the Magnetic Flux Through the Coil**:
The area \( A \) of the circular coil of radius \( 2R \) is:
\[
A = \pi (2R)^2 = 4\pi R^2
\]
The magnetic flux \( \Phi \) through the coil is given by:
\[
\Phi(t) = B(t) \cdot A = \mu_0 n (k t e^{-\alpha t}) \cdot (4\pi R^2)
\]
Therefore,
\[
\Phi(t) = 4\pi \mu_0 n k t R^2 e^{-\alpha t}
\]
4. **Apply Faraday's Law of Induction**:
According to Faraday's law, the induced emf \( \mathcal{E} \) in the coil is the negative rate of change of magnetic flux:
\[
\mathcal{E} = -\frac{d\Phi}{dt}
\]
5. **Differentiate the Flux**:
To find the induced emf, we differentiate \( \Phi(t) \):
\[
\frac{d\Phi}{dt} = 4\pi \mu_0 n R^2 \left( k e^{-\alpha t} - k \alpha t e^{-\alpha t} \right)
\]
Simplifying this gives:
\[
\frac{d\Phi}{dt} = 4\pi \mu_0 n R^2 k e^{-\alpha t} (1 - \alpha t)
\]
Thus, the induced emf is:
\[
\mathcal{E} = -4\pi \mu_0 n R^2 k e^{-\alpha t} (1 - \alpha t)
\]
6. **Determine the Induced Current**:
If the resistance of the coil is \( R_c \), the induced current \( I_{ind} \) can be expressed as:
\[
I_{ind} = \frac{\mathcal{E}}{R_c} = -\frac{4\pi \mu_0 n R^2 k e^{-\alpha t} (1 - \alpha t)}{R_c}
\]
7. **Analyze the Behavior of the Induced Current**:
- At \( t = 0 \):
\[
I_{ind}(0) = -\frac{4\pi \mu_0 n R^2 k}{R_c}
\]
- At \( t = 1/\alpha \) (where \( 1 - \alpha t = 0 \)):
\[
I_{ind}(1/\alpha) = 0
\]
- As \( t \to \infty \):
\[
I_{ind} \to 0
\]
### Conclusion:
The induced current starts at a negative value, becomes zero at \( t = 1/\alpha \), and approaches zero as \( t \) increases. The correct depiction of the induced current as a function of time is represented by a curve that starts negative, crosses zero, and approaches zero again.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
A long solenoid of radius R carries a time (t) – dependent current I=I_(0)(t-2t^(2)) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30^(@) with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A long solenoid of radius R carries a time (t) – dependent current I=I_(0)(t-2t^(2)) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30^(@) with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
A circular coil of 25 turns and radius of 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of coil. If the current in the coil is 5 A, then total torque experienced by the coil is
A current I flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field, magnitude of the torque that acts on the coil is
A non uniform magnetic field B=B_(0)that"i" in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
A current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
A circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is