A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
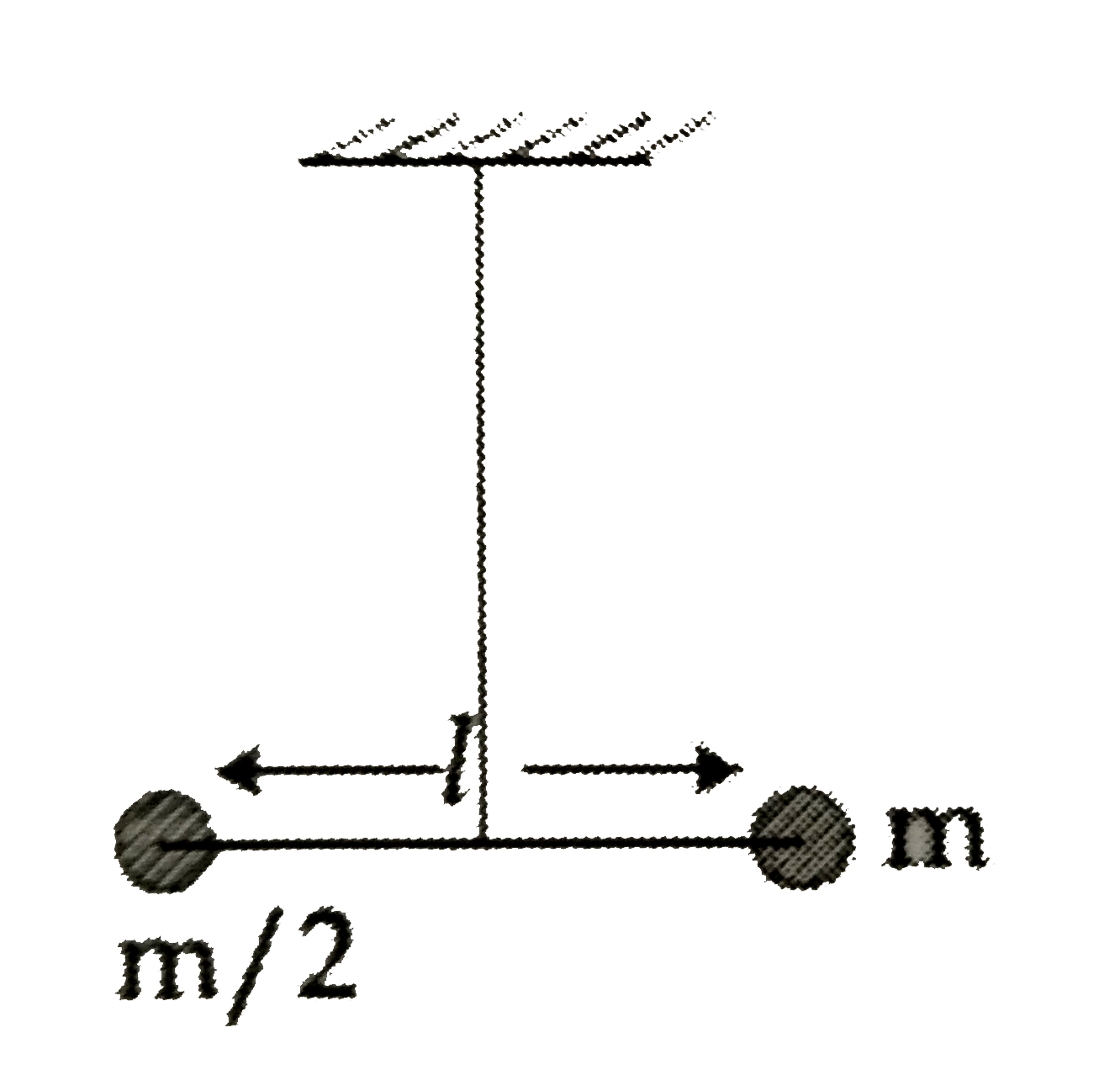
- Two masses m and (m)/(2) are connected at the two ends of a massless r...
Text Solution
|
- A uniform rod of mass m and length l is suspended through a light wire...
Text Solution
|
- Two small balls, each of mass m are connected by a light rigid rod of ...
Text Solution
|
- Two particles , each of mass m and charge q, are attached to the two ...
Text Solution
|
- As shown in the figure, two blocks, each of mass m, suspended from the...
Text Solution
|
- Two masses m and (m)/(2) are connected at the two ends of a massless r...
Text Solution
|
- चित्र 22.5 में द्रव्यमान m एवं लम्बाई l वाली एक समरूप छड़ को लम्बाई l व...
Text Solution
|
- A thin uniform rod of mass M and length L is rotating about a perpendi...
Text Solution
|
- A thin rod of mass m and length l is rotated in a horizontal plane ab...
Text Solution
|