A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
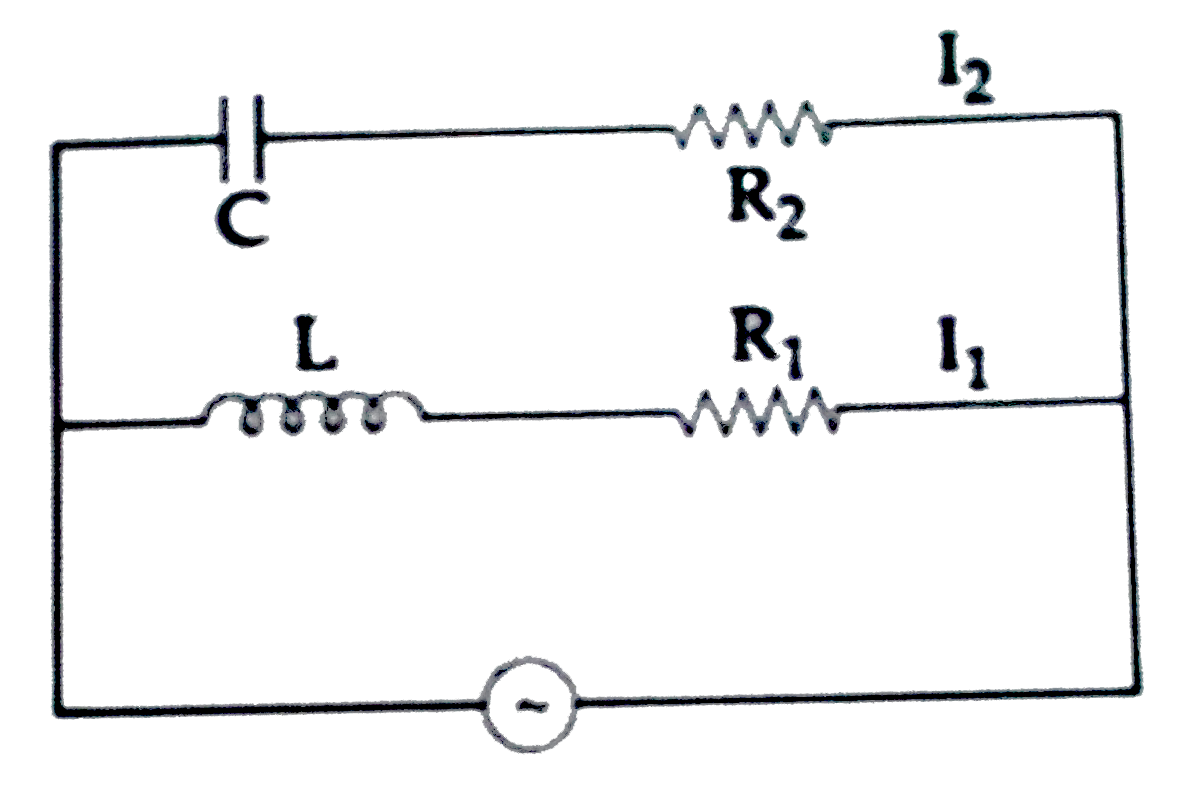
- In the value circuit, C=(sqrt(3))/(2)muF,R2=20Omega, L=sqrt(3)/(10)H, ...
Text Solution
|
- In the circuit shown in figure R1=30Omega, R2=40 Omega, L=0.4H and C=1...
Text Solution
|
- In the following circuit ,E1 = 4V, R1 = 2 Omega, E2 = 6 V, R2 = 2Oem...
Text Solution
|
- In the given circuit, if I1 and I2 be the current in resistances R1 an...
Text Solution
|
- The photo electric current at distances r1 and r2 of light source from...
Text Solution
|
- In the value circuit, C=(sqrt(3))/(2)muF,R2=20omega, L=sqrt(3)/(10)H, ...
Text Solution
|
- In the value circuit, C=(sqrt(3))/(2)muF,R2=20omega, L=sqrt(3)/(10)H ,...
Text Solution
|
- Current versus voltage (I – v) graphs for two different series L–C–R c...
Text Solution
|
- एक शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल pi l (r1 + r2) है, जहाँ l...
Text Solution
|