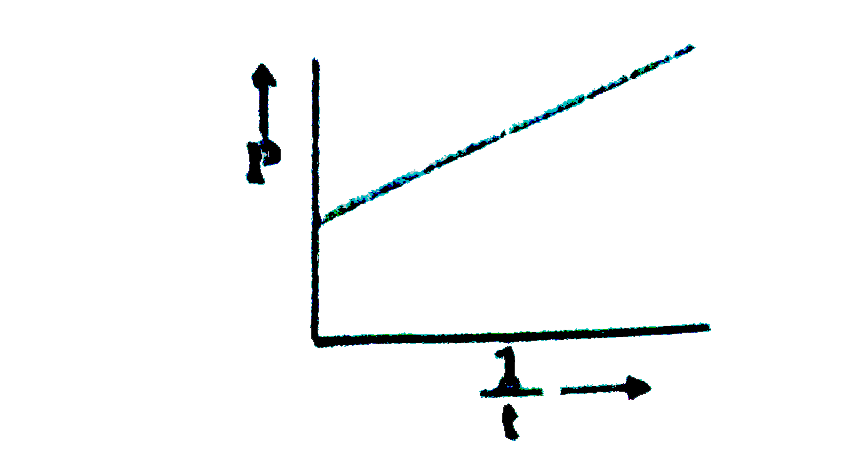
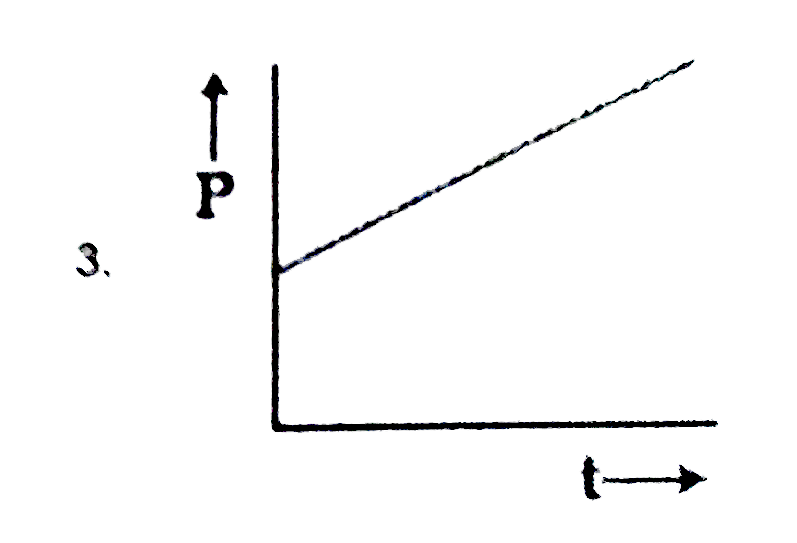
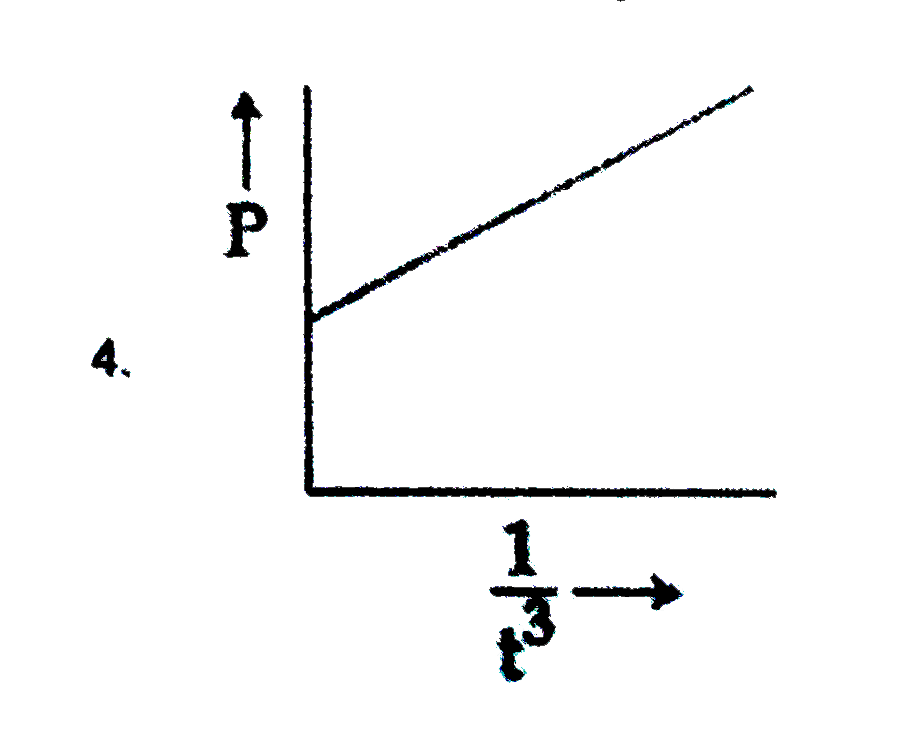A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A soap bubble is blown with the help of mechanical pump at the mouth o...
Text Solution
|
- The execc pressure inside the first soap bubble is three times that in...
Text Solution
|
- A soap bubble is blown with the help of mechanical pump at the mouth o...
Text Solution
|
- The soap bubble formed at the end of the tube is blown very slowly. Dr...
Text Solution
|
- The excess pressure inside a soap bubble is thrice the excess pressure...
Text Solution
|
- Two soap bubbles are blown. In first soap bubble excess pressure is 4 ...
Text Solution
|
- A soap bubble,blown by a mechanical pump at the mouth of a tube, incre...
Text Solution
|
- An air bubble just inside a soap solution and a soap bubble blown usin...
Text Solution
|
- The excess pressure inside a soap bubble of volume V is P . Then exces...
Text Solution
|