Consider a rubber ball freely falling from a height ` h = 4.9 m` onto a horizontally elastic plate. Assume that the duration of collision is negligible and the collisions with the plate is totally elastic .
Then the velocity as a function of time and the height as a function of time will be :
Consider a rubber ball freely falling from a height ` h = 4.9 m` onto a horizontally elastic plate. Assume that the duration of collision is negligible and the collisions with the plate is totally elastic .
Then the velocity as a function of time and the height as a function of time will be :
Then the velocity as a function of time and the height as a function of time will be :
A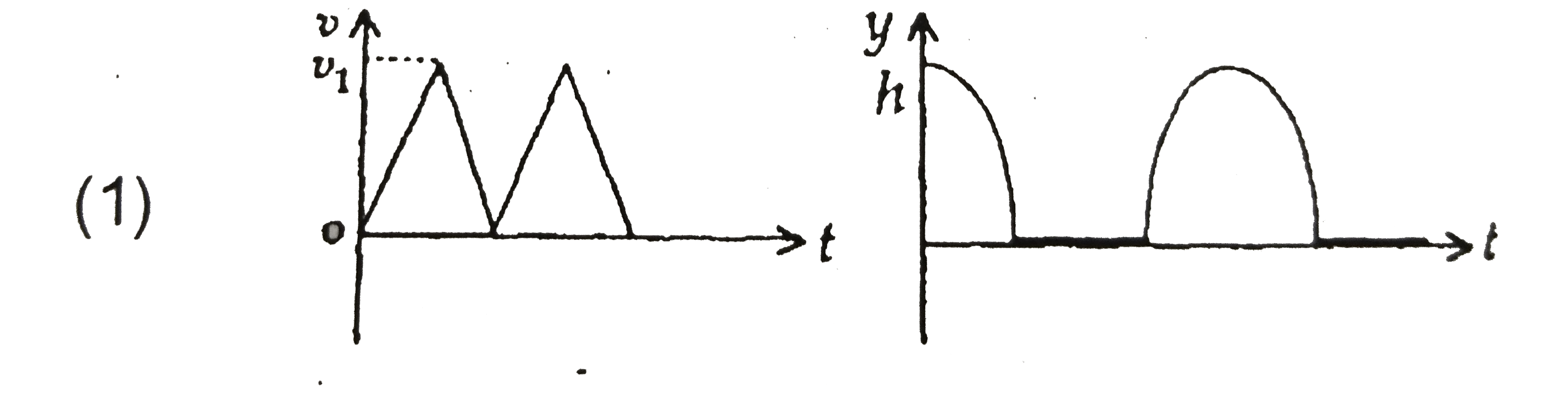

B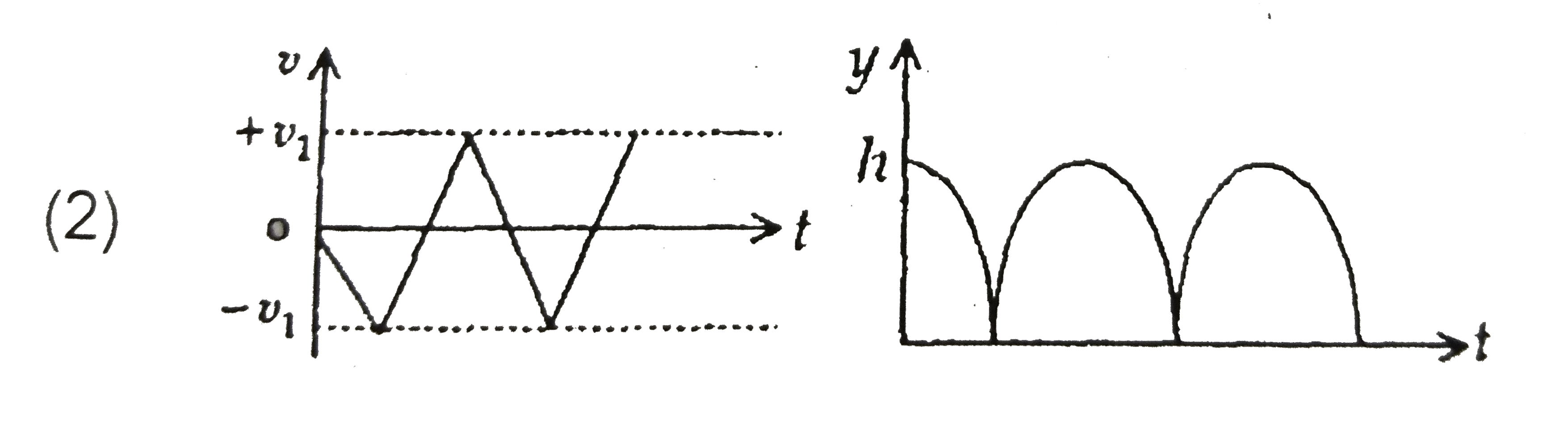
C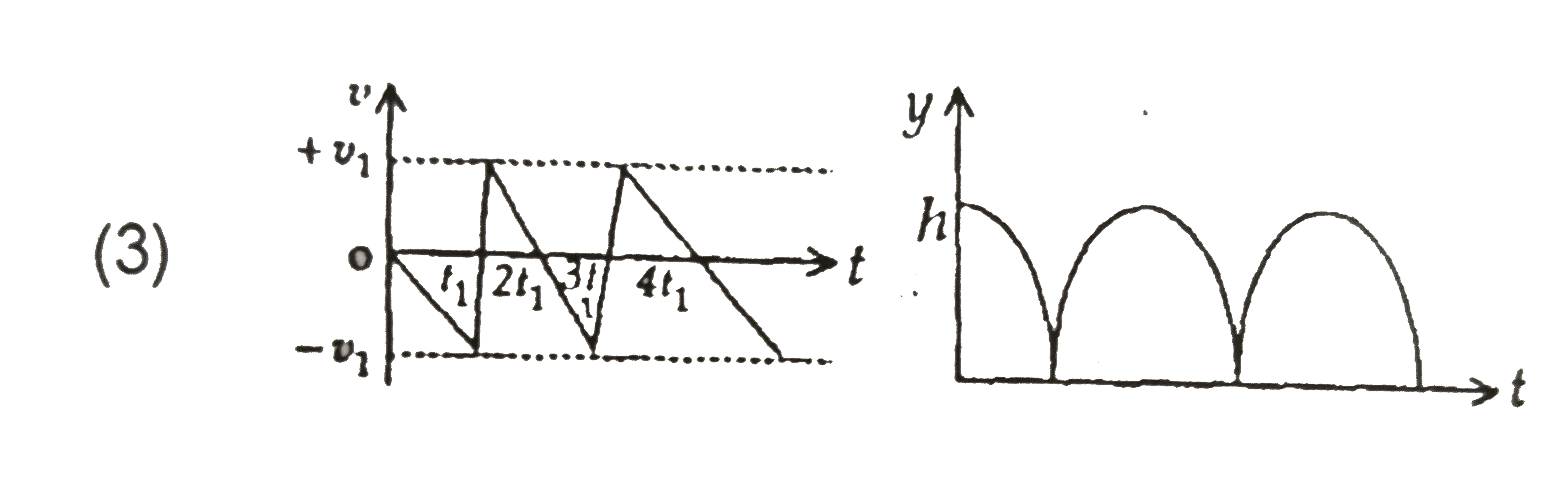
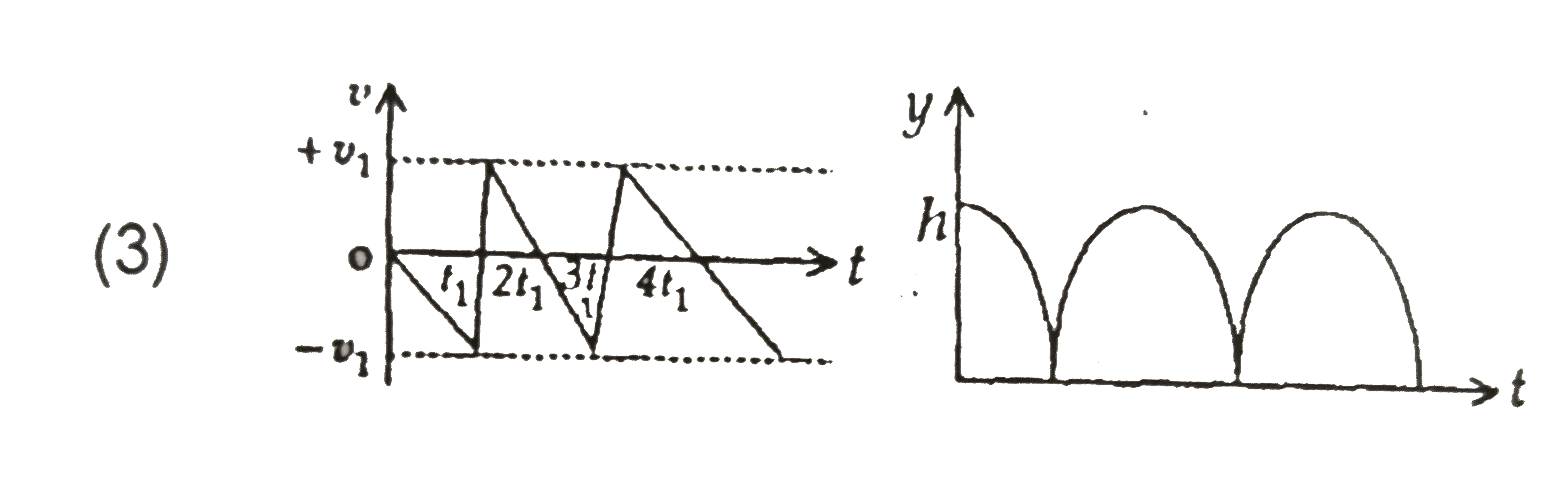
D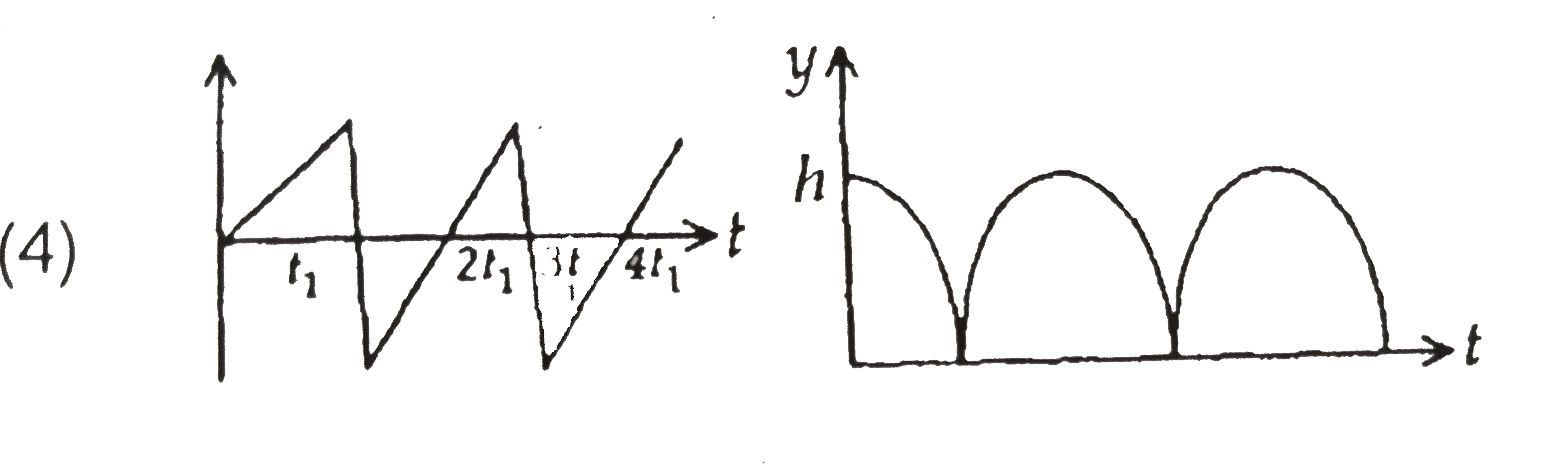
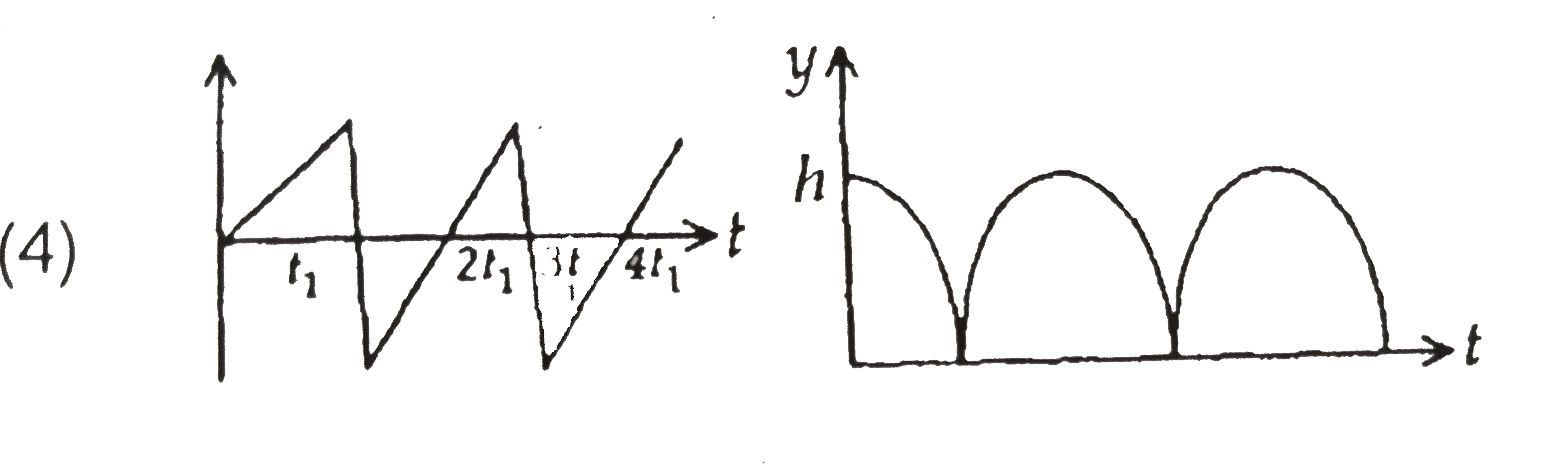
Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem of a rubber ball falling from a height of \( h = 4.9 \, \text{m} \) onto a horizontally elastic plate, we need to determine the velocity and height of the ball as functions of time.
### Step-by-Step Solution:
1. **Understanding the Initial Conditions**:
- The ball is dropped from rest, so its initial velocity \( u = 0 \).
- The height from which it is dropped is \( h = 4.9 \, \text{m} \).
2. **Using the Kinematic Equation for Velocity**:
- The equation for the velocity of an object under free fall is given by:
\[
v = u + at
\]
- Here, \( a = -g \) (acceleration due to gravity, negative because it is directed downwards), and \( g \approx 9.8 \, \text{m/s}^2 \).
- Substituting \( u = 0 \):
\[
v = 0 - gt = -gt
\]
- Therefore, the velocity as a function of time is:
\[
v(t) = -9.8t \quad \text{(for the downward motion)}
\]
3. **Calculating the Time of Fall**:
- To find the time \( t \) it takes to fall \( 4.9 \, \text{m} \), we use the second kinematic equation:
\[
s = ut + \frac{1}{2}at^2
\]
- Here, \( s = -4.9 \, \text{m} \) (since it falls down), \( u = 0 \), and \( a = -g \):
\[
-4.9 = 0 + \frac{1}{2}(-9.8)t^2
\]
- Simplifying gives:
\[
-4.9 = -4.9t^2 \quad \Rightarrow \quad t^2 = 1 \quad \Rightarrow \quad t = 1 \, \text{s}
\]
4. **Behavior During the Collision**:
- Since the collision with the elastic plate is perfectly elastic, the ball will rebound with the same speed but in the opposite direction.
- Therefore, after \( t = 1 \, \text{s} \), the velocity will be:
\[
v = 9.8 \, \text{m/s} \quad \text{(upward)}
\]
5. **Height as a Function of Time**:
- For the upward motion after the collision, we again use the kinematic equation:
\[
s = ut + \frac{1}{2}at^2
\]
- For the upward motion, the initial velocity \( u = 9.8 \, \text{m/s} \) and \( a = -g \):
\[
h(t) = 4.9 + 9.8t - \frac{1}{2}(9.8)t^2
\]
- This will continue until the ball reaches the maximum height and then falls back down.
6. **Generalizing the Motion**:
- The ball will continue to bounce indefinitely, following the same pattern of falling and rebounding, maintaining the same height of \( 4.9 \, \text{m} \) for each bounce.
### Final Functions:
- **Velocity as a function of time**:
\[
v(t) =
\begin{cases}
-9.8t & \text{for } 0 \leq t < 1 \\
9.8(t - 2n) & \text{for } t \text{ in the } n^{th} \text{ bounce}
\end{cases}
\]
- **Height as a function of time**:
\[
h(t) =
\begin{cases}
4.9 - \frac{1}{2}gt^2 & \text{for } 0 \leq t < 1 \\
4.9 + 9.8(t - 2n) - \frac{1}{2}g(t - 2n)^2 & \text{for } t \text{ in the } n^{th} \text{ bounce}
\end{cases}
\]
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 3/4 , the ball will strike second time with the plane after
A ball after freely falling from a height of 4.9m strikes a horizontal plane. If the coefficient of restitution is 3/4 , the ball will strike second time with the plane after
A ball starts falling freely from a height h from a point on the inclined plane forming an angle alpha with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
A metal ball falls from a height of 1m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball and steel plate is
A ball falls under gravity from a height of 10 m with an initial downward velocity u. It collides with the ground, losses 50% of its energy in collision and then rises back to the same height. The initial velocity u is
A ball is projected vertically down with an initial velocity from a height of 20 m onto a horizontal floor. During the impact it loses 50% of its energy and rebounds to the same height. The initial velocity of its projection is
A ball is let fall from a height h_(0) . There are n collisions with the earth. If the velocity of rebound after n collisions is v_(n) and the ball rises to a height h_(n) then coefficient of restitution e is given by
A ball is let fall from a height h_(0) . There are n collisions with the earth. If the velocity of rebound after n collision is v_(n) and the ball rises to a height h_(n) then coefficient of restitution e is given by
A ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is
A ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is