In a uniformly charged sphere of total charge Q and radius R, the electric field E is plotted as function of distance from the centre, The graph which would correspond to the above will be:
In a uniformly charged sphere of total charge Q and radius R, the electric field E is plotted as function of distance from the centre, The graph which would correspond to the above will be:
A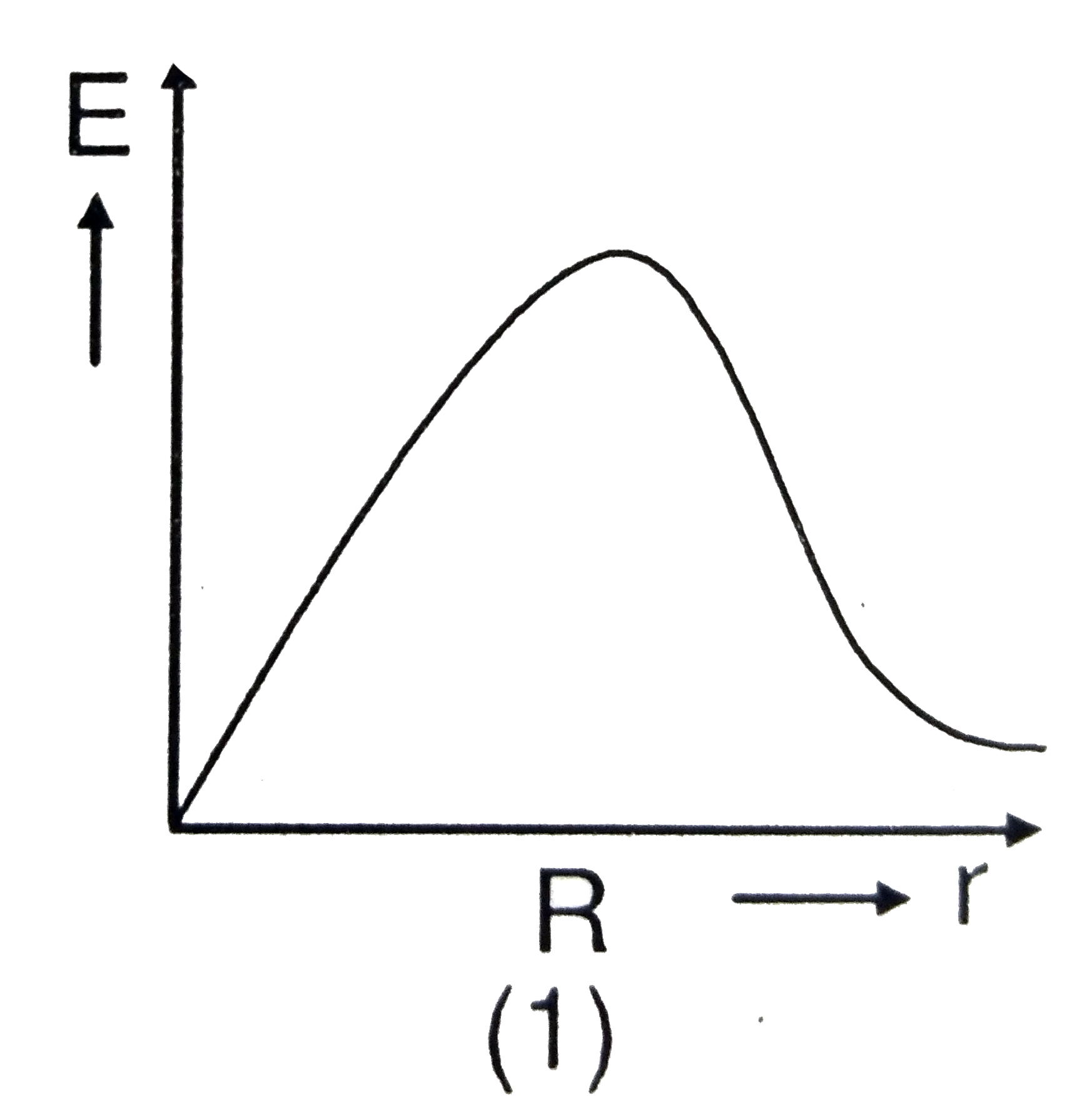

B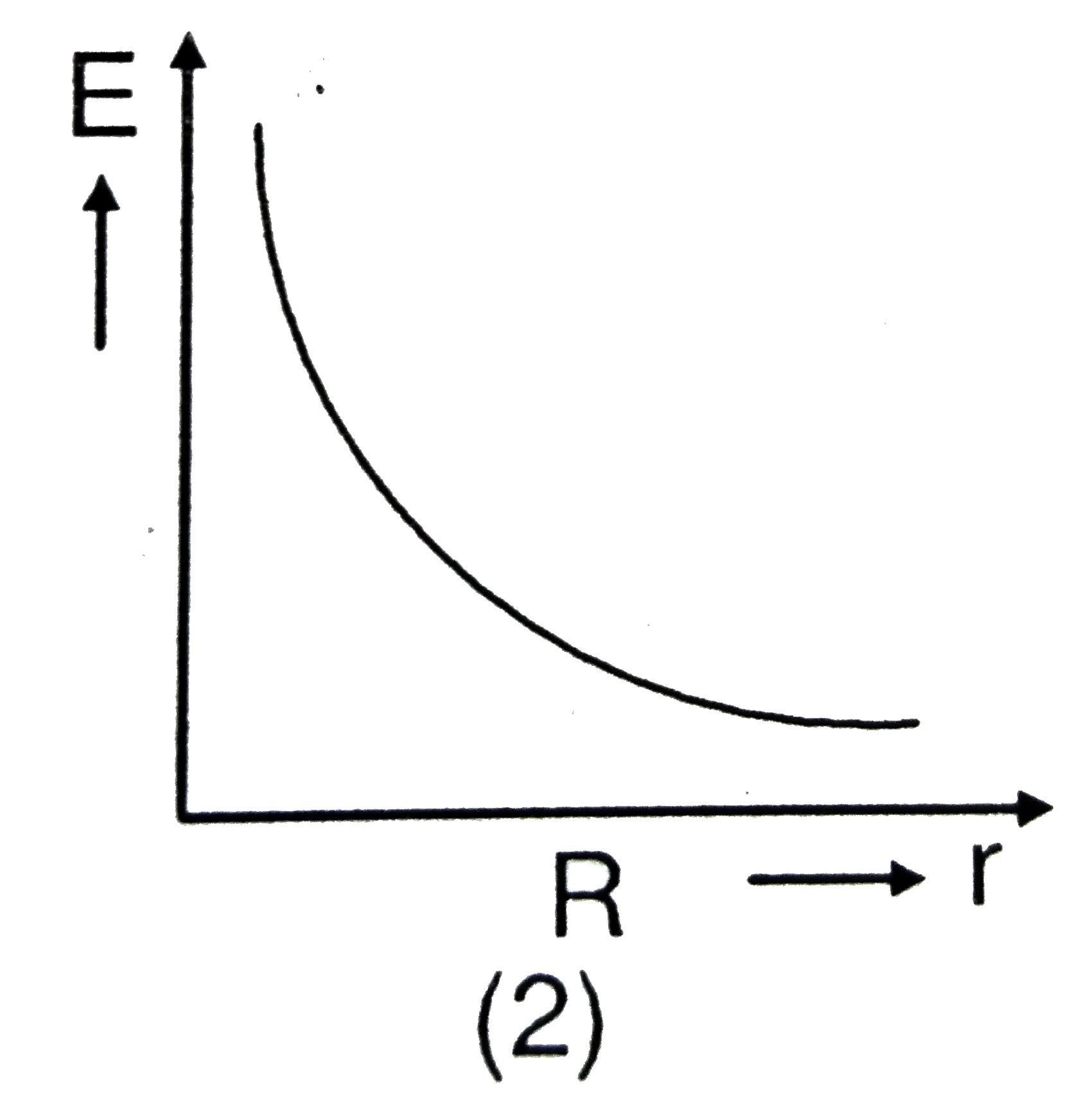

C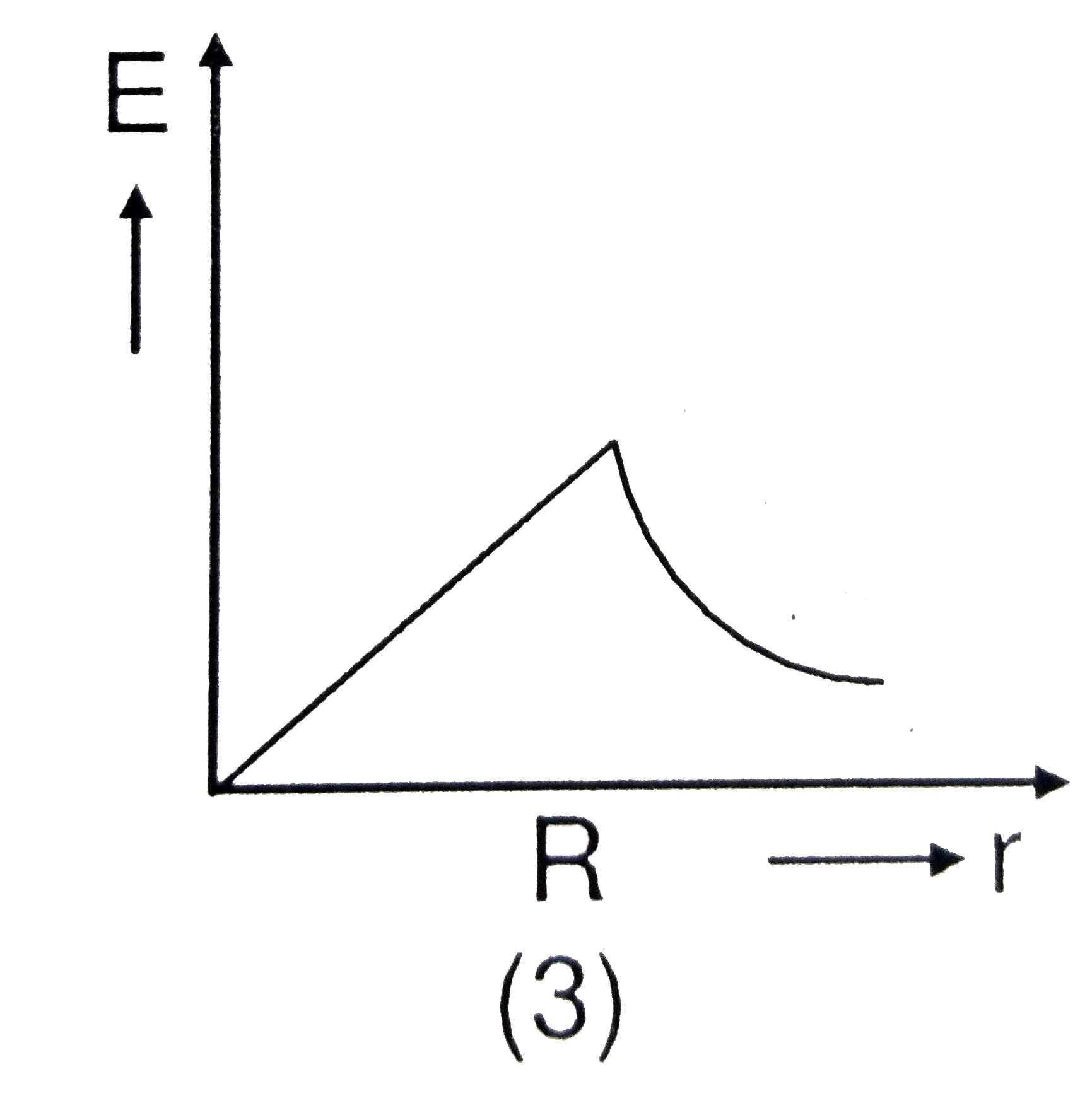

D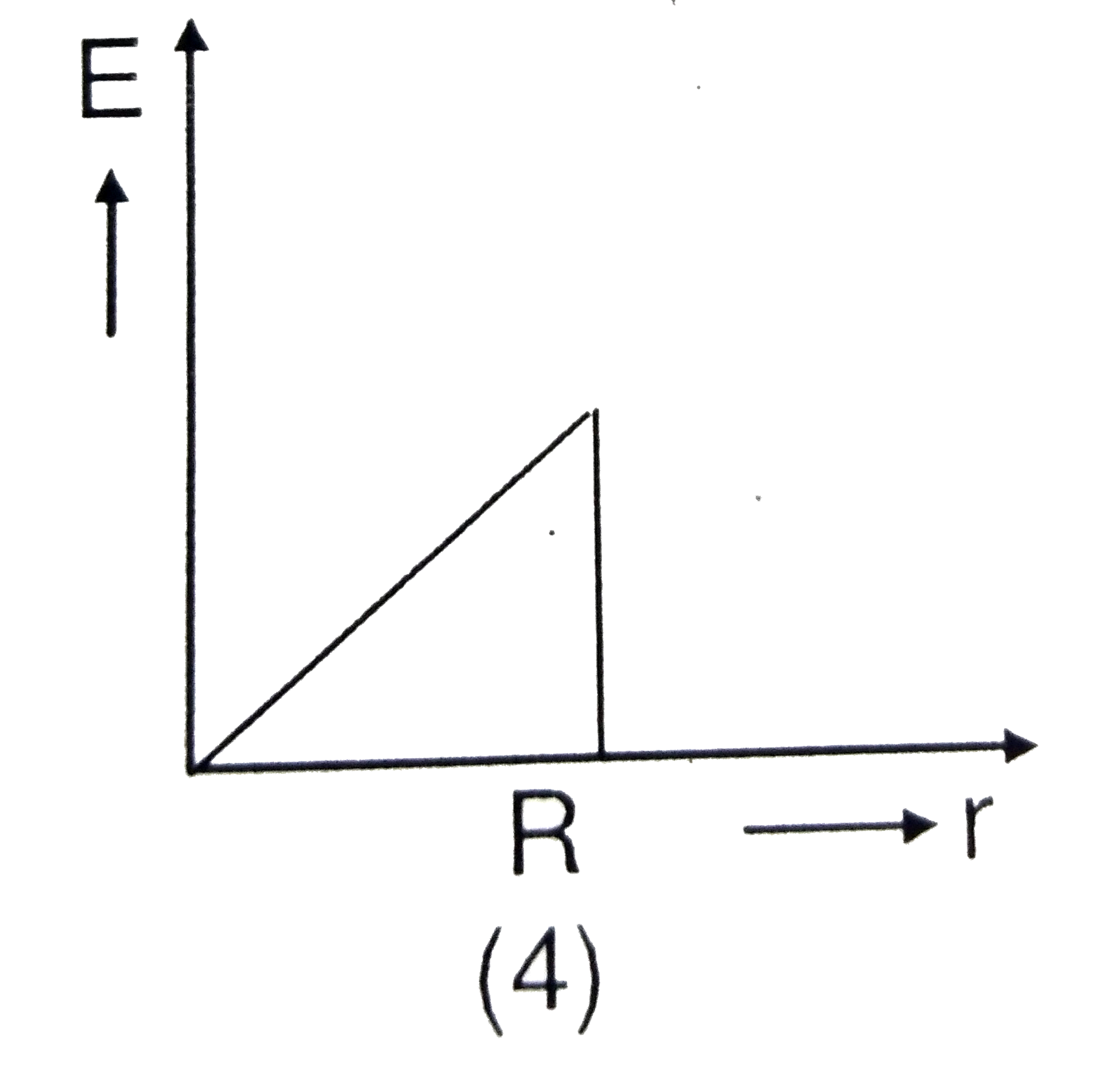

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem of finding the electric field \( E \) as a function of distance from the center of a uniformly charged sphere with total charge \( Q \) and radius \( R \), we will analyze the electric field both inside and outside the sphere using Gauss's law.
### Step-by-Step Solution:
1. **Understanding the Problem**:
We have a uniformly charged sphere with total charge \( Q \) and radius \( R \). We need to determine how the electric field \( E \) varies with distance \( r \) from the center of the sphere.
2. **Electric Field Inside the Sphere**:
For points inside the sphere (where \( r < R \)):
- According to Gauss's law, the electric field \( E \) at a distance \( r \) from the center can be calculated using a Gaussian surface of radius \( r \).
- The charge enclosed by this Gaussian surface is given by:
\[
Q_{\text{enc}} = \rho \cdot V = \rho \cdot \frac{4}{3} \pi r^3
\]
where \( \rho \) is the charge density and \( V \) is the volume of the sphere of radius \( r \).
- The charge density \( \rho \) can be expressed as:
\[
\rho = \frac{Q}{\frac{4}{3} \pi R^3}
\]
- Substituting this into the expression for \( Q_{\text{enc}} \):
\[
Q_{\text{enc}} = \frac{Q}{\frac{4}{3} \pi R^3} \cdot \frac{4}{3} \pi r^3 = Q \cdot \frac{r^3}{R^3}
\]
- Applying Gauss's law:
\[
E \cdot 4 \pi r^2 = \frac{Q_{\text{enc}}}{\epsilon_0}
\]
- Therefore:
\[
E \cdot 4 \pi r^2 = \frac{Q \cdot \frac{r^3}{R^3}}{\epsilon_0}
\]
- Solving for \( E \):
\[
E = \frac{Q}{4 \pi \epsilon_0 R^3} r
\]
- This shows that the electric field inside the sphere increases linearly with \( r \).
3. **Electric Field Outside the Sphere**:
For points outside the sphere (where \( r \geq R \)):
- The entire charge \( Q \) can be treated as if it were concentrated at the center of the sphere.
- Thus, the electric field \( E \) at a distance \( r \) is given by:
\[
E = \frac{Q}{4 \pi \epsilon_0 r^2}
\]
- This indicates that the electric field decreases with the square of the distance from the center.
4. **Graphical Representation**:
- For \( r < R \), the electric field \( E \) increases linearly from \( 0 \) to a maximum value at \( r = R \).
- For \( r \geq R \), the electric field \( E \) decreases with \( \frac{1}{r^2} \).
- Therefore, the graph of \( E \) as a function of \( r \) will show a linear increase for \( r < R \) and a hyperbolic decrease for \( r \geq R \).
5. **Conclusion**:
The correct graph corresponding to the electric field \( E \) as a function of distance \( r \) from the center of the uniformly charged sphere will show a linear increase for \( r < R \) and a \( \frac{1}{r^2} \) decrease for \( r \geq R \).
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
For a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
A solid sphere of radius R is charged uniformly. The electrostatic potential V is plotted as a function of distance r from the centre of th sphere. Which of the following best represents the resulting curve?
If the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (rgtR) .
Figure shows a uniformly charged thin non-conducting sphere of total charge Q and radius R. If point charge q is situated at point 'A' which is at a distance r lt R from centre of the sphere, then find out following : (i) Force acting on charge q. (ii) Electric field at centre of sphere. (iii) Electric field at point B.
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
At a point 20 cm from the centre of a uniformly charged dielectric sphere of radius 10 cm , the electric field is 100 V//m . The electric field at 3 cm from the centre of the sphere will be
A non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
The diagram shows a uniformly charged bemisphere of radius R. It has volume charge density rho . If the electric field at a point 2R distance below its centre ?