A charge `Q` is uniformly distributed over the surface of non - conducting disc of radius `R`. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A charge `Q` is uniformly distributed over the surface of non - conducting disc of radius `R`. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A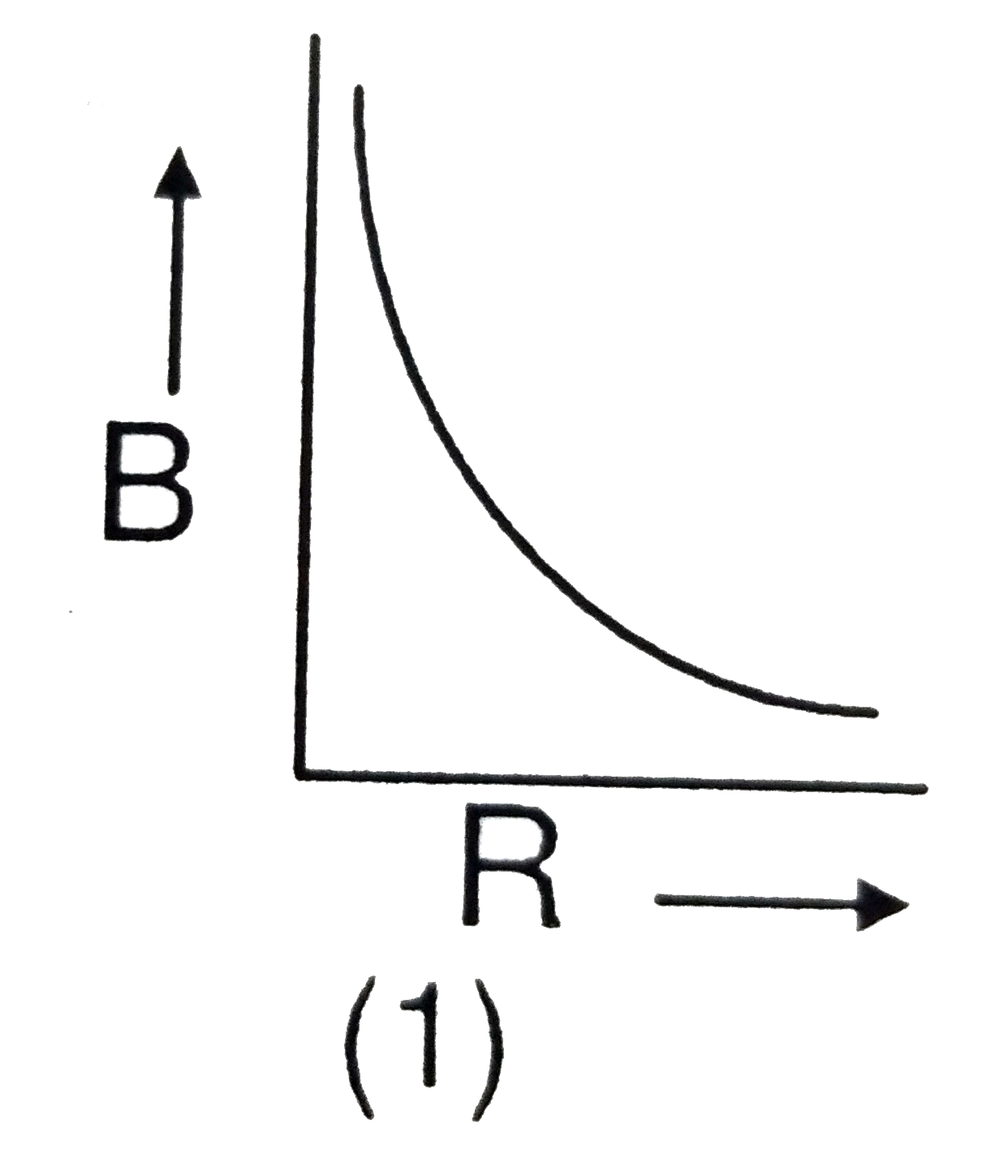

B

C

D

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem step by step, we will analyze the magnetic field at the center of a rotating non-conducting disc with a uniformly distributed charge \( Q \) over its surface.
### Step 1: Understanding the Setup
We have a non-conducting disc of radius \( R \) with a total charge \( Q \) uniformly distributed over its surface. The disc rotates about an axis perpendicular to its plane and passing through its center with a constant angular velocity \( \omega \).
### Step 2: Consider an Elemental Ring
To find the magnetic field at the center of the disc, we can consider an elemental ring of thickness \( dr \) at a distance \( r \) from the center of the disc. The area of this elemental ring is given by:
\[
dA = 2 \pi r \, dr
\]
### Step 3: Charge on the Elemental Ring
The surface charge density \( \sigma \) is defined as:
\[
\sigma = \frac{Q}{\pi R^2}
\]
The charge \( dQ \) on the elemental ring can be expressed as:
\[
dQ = \sigma \, dA = \sigma \cdot 2 \pi r \, dr = \frac{Q}{\pi R^2} \cdot 2 \pi r \, dr = \frac{2Qr}{R^2} \, dr
\]
### Step 4: Current Due to Rotation
The current \( I \) associated with the rotating ring can be calculated. The time period \( T \) for one complete rotation is given by:
\[
T = \frac{2\pi}{\omega}
\]
Thus, the current \( I \) through the ring is:
\[
I = \frac{dQ}{T} = \frac{dQ \cdot \omega}{2\pi} = \frac{2Qr}{R^2} \cdot \frac{\omega}{2\pi} \, dr = \frac{Qr\omega}{\pi R^2} \, dr
\]
### Step 5: Magnetic Field Contribution from the Elemental Ring
The magnetic field \( dB \) at the center of the disc due to the current \( I \) in the elemental ring is given by:
\[
dB = \frac{\mu_0 I}{2r}
\]
Substituting the expression for \( I \):
\[
dB = \frac{\mu_0}{2r} \cdot \frac{Qr\omega}{\pi R^2} \, dr = \frac{\mu_0 Q \omega}{2\pi R^2} \, dr
\]
### Step 6: Total Magnetic Field at the Center
To find the total magnetic field \( B \) at the center of the disc, we integrate \( dB \) from \( r = 0 \) to \( r = R \):
\[
B = \int_0^R dB = \int_0^R \frac{\mu_0 Q \omega}{2\pi R^2} \, dr = \frac{\mu_0 Q \omega}{2\pi R^2} \cdot R = \frac{\mu_0 Q \omega}{2\pi R}
\]
### Step 7: Analyzing the Variation of Magnetic Field with Radius
From the expression we derived, we see that the magnetic field \( B \) is inversely proportional to the radius \( R \):
\[
B \propto \frac{1}{R}
\]
This indicates that as the radius \( R \) increases, the magnetic field \( B \) at the center decreases.
### Conclusion
The variation of the magnetic induction \( B \) at the center of the disc as the radius \( R \) changes, while keeping \( Q \) and \( \omega \) constant, will be represented by a hyperbolic relationship, confirming that \( B \) decreases as \( R \) increases.
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A charge q is uniformly distributed on a non-conducting disc of radius R . It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
Circular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity omega . Its K.E . Is
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
A metal disc of radius R rotates with an angular velcoity omega about an axis perpendiclar to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
A round disc of moment of inertia I_2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I_1 rotating with an angular velocity omega about the same axis. The final angular velocity of the combination of discs is.
If a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
A nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity omega . The magnt moment of this disc is .
A disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is