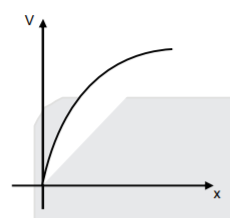
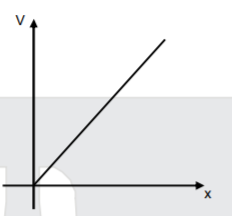
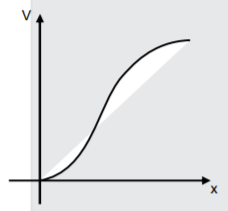
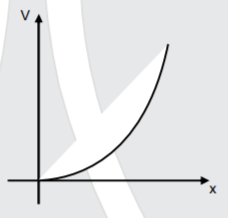
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
JEE MAINS PREVIOUS YEAR ENGLISH-JEE MAIN-All Questions
- In the given circuit switch is closed at t = 0. The charge flown in ti...
Text Solution
|
- A particle is dropped from height h = 100 m, from surface of a planet....
Text Solution
|
- A charge particle of mass m and charge q is released from rest in unif...
Text Solution
|
- An object is gradually moving away from the focal point of a concave m...
Text Solution
|
- In full scale deflection current in galvanometer of 100 ohm resistance...
Text Solution
|
- There are two identical particles A and B. One is projected vertically...
Text Solution
|
- The length of a pendulum is measured as 20.0 cm. The time interval for...
Text Solution
|
- An electron is moving initially with velocity vo hati+vohatj in unifor...
Text Solution
|
- An asteroid of mass m (m lt lt mE) is approaching with a velocity 12 k...
Text Solution
|
- In H–spectrum wavelength of 1^(st) line of Balmer series is lambda= 65...
Text Solution
|
- Two batteries (connected in series) of same emf 10 V of internal resis...
Text Solution
|
- An EMW is travelling along z-axis vecB=5 xx 10^(-8) hatj T, C=3 xx 10^...
Text Solution
|
- Kinetic energy of the particle is E and it's De-Broglie wavelength is ...
Text Solution
|
- The dimensional formula of sqrt((hc^5)/G) is
Text Solution
|
- Two immiscible liquids of refractive index sqrt 2 and 2sqrt2 are fille...
Text Solution
|
- The identical solid sphere each having mass m and diameter d are touch...
Text Solution
|
- A solid sphere having radius R and uniform charge density rho has a ca...
Text Solution
|
- Consider an infinitely long current carrying cylindrical straight wire...
Text Solution
|
- Find current in the wire BC.
Text Solution
|
- Electric field and magnetic field in a region of space are given by(Ē=...
Text Solution
|