Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SL ARORA-Mathematical tools-Exercise
- Evaluate , where M and l are constants.
Text Solution
|
- Find dy/dx for the following functions:y= x^3- 3x^2 + 3x - (2/5).
Text Solution
|
- Find dy/dx for the following functions:y= ((x-1)(x-2))/sqrtx.
Text Solution
|
- Find dy/dx for the following functions: y= (sqrt x + (1/sqrt x))^2.
Text Solution
|
- Differentiate the following functions: (x^2 -4x +5)(x^3 -2).
Text Solution
|
- Differentiate the following functions:((2x +3)/(x^2-5)).
Text Solution
|
- Differentiate the following functions: ((sin x+ cosx)/(sin x - cos x).
Text Solution
|
- Differentiate the following functions: (4x^3 - 5x^2 + 1)^4.
Text Solution
|
- If the motion of aparticle is governed by the equation, s= 2t^3- 3t^2+...
Text Solution
|
- The angular displacement of a particle performing circular motion is ...
Text Solution
|
- Show that force can be expressed as the product of mass and accelerati...
Text Solution
|
- Integrate the following: 6x + 5x^2 - 2x^3 + (1/x^2)
Text Solution
|
- Integrate the following: ax^2 +bx+c
Text Solution
|
- Integrate the following:(x+(1/x))^3
Text Solution
|
- Integrate the following: 3 cosec^2 x- 5x+ sinx)
Text Solution
|
- Integrate the following: 3cosec^2 x +2sin 3x)
Text Solution
|
- Evaluate the following integrals:
Text Solution
|
- Evaluate the following integrals:
Text Solution
|
- Evaluate the following integrals:
Text Solution
|
- Evaluate the following integrals:
Text Solution
|
- Evaluate the following integrals:
Text Solution
|
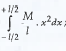 , where M and l are constants.
, where M and l are constants.