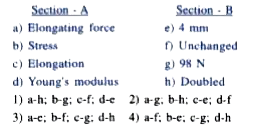Home
Class 11
PHYSICS
A spring of young's modulus 2 xx 10^11 ...

A spring of young's modulus `2 xx 10^11` pa is suspended vertically and subjected to a load of 5 kg and elongation is 2 mm. when the load is doubled - match the following `(g = 9.8 m//s^2)`

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH SERIES|Exercise EXERCISE -IA (ASCENDING OR DESCENDING ORDER)|4 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH SERIES|Exercise EXERCISE IB (ASSERTION (A) AND REASON ( R) TYPE QUESTIONS (STRESS; STRAIN ; ELASTICITY; YOUNGS MODULUS))|26 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH SERIES|Exercise EXERCISE -IA|60 Videos

  • MECHANICAL PROPERTIES OF FLUIDS

    AAKASH SERIES|Exercise EXERCISE-3|43 Videos

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise Practice Exercise|84 Videos

Similar Questions

Explore conceptually related problems

A load of 1 kg weight is a attached to one end of a steel wire of area of cros-section 3 mm^(2) and Young's modulus 10^11 Nm^-2 . The other end is suspended vertically from a hook on a wall, then the load is pulled horizontally and released. When the load passes through its lowest position the fractional change in length is (10ms^-2)

A uniform rectangular block of mass 50 kg is hung horizontally with the help of three wires A, B and C each of length and area of 2 m and 10 mm^2 respectively as shown in the figure. The central wire is passing through the centre of gravity and is made of a material of Young's modulus 7.5 xx 10^10 Nm^(-2) and the other two wires A and C symmetrically placed on either side of the wire B are of Young's modulus 10^11 Nm^(-2) . The tension in the wires A and B will be in the ratio of

A horizontal aluminium rod of diameter 4 cm projected 6 cm from a wall . An object of mass 400 pi kg is suspended from the end of the rod. The shearing modulus of aluminium is 3.0xx10^(10)N//m^(2) . The vertical deflection of the end of the rod is ( :' g = 10 m//s^(2) )