Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
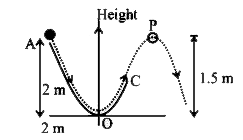
- A particle (m = 3 kg) slides down a frictionless track (AOC) starting ...
Text Solution
|
- A particle of mass m=5.00kg is released from point A and it slides on ...
Text Solution
|
- A particle of mass m slides on a frictionaless surface ABCD, starting ...
Text Solution
|
- A particle slides down a frictionless paraboli (y=x^(2)) track (A-B-C)...
Text Solution
|
- A particle (m = 1kg) slides down a frictionless track (AOC) starting f...
Text Solution
|
- A particle (m = 2 kg) slides down a smooth track AOC starting from res...
Text Solution
|
- A particle (m = 3 kg) slides down a frictionless track (AOC) starting ...
Text Solution
|
- A particle slides down a frictionless paraboli (y=x^(2)) track (A-B-C)...
Text Solution
|
- A Particle slides down a frictionless parabolic (y=x^(2)0 track (AtoB...
Text Solution
|