Home
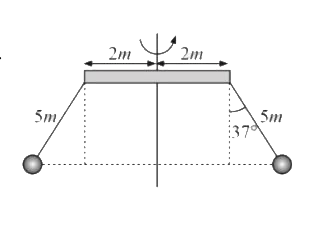
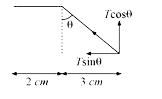
Class 12
PHYSICS
Two identical small balls are suspended ...

Two identical small balls are suspended by ends of a rod. Whole assembly is rotating about vertical axis passing through center of rod. At a certain value of `omega` both strings make 37° with vertical. Find `omega`

A

`sqrt((2)/(3))` rad/sec

B

`sqrt((7)/(3))` rad/sec

C

`sqrt((3)/(2))` rad/sec

D

`sqrt((5)/(2))` rad/sec

Text Solution

Verified by Experts

The correct Answer is:
C

`T cos theta=mg`
`T sin theta=m omega^(2)r`
`tan theta=(omega^(2)5)/(g)`
`omega=sqrt((3)/(2))`rad/sec
Promotional Banner

Similar Questions

Explore conceptually related problems

A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.

A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is

Two balls of masses m_(1) = 0.5 kg and m_(2) = 0.3 kg are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with omega = 110 rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if l=20 cm is the length of the string. Is the equilibrium of the balls stable ?

A uniform rod of length l , mass m , cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity omega . Find the total extension in the rod due to the tension produced in the rod.

A uniform rod of mass m and length L lies radialy on a disc rotating with angular speed omega in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

Three identical thin rods, each of length L and mass m , are welded perpendicular to one another as shown in figure. The assembly is rotated about an axis that passes through the end of one rod and is parallel to another. The moment of inertia of this structure about this axis is. .

A thin uniform heavy rod of length l hangs from a horizontal axis passing through one end. The initial angular velocity omega that must be imparted to it to rotate it through 90^(@) is :

A uniform rod of mass m and length l_(0) is rotating with a constant angular speed omega about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle theta to the vertical (axis of rotation).

A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.