Home
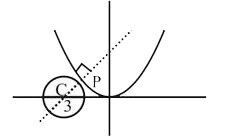
Class 12
MATHS
Let P be a point on parabola x ^ 2 ...

Let P be a point on parabola ` x ^ 2 = 4y ` . If the distance of P from the centre of circle ` x ^ 2 + y ^ 2 + 6x + 8 = 0 ` is minimum, then the equation of tangent at P on parabola ` x ^ 2 = 4y ` is :

A

`x+y+1=0`

B

`x+y-1=0`

C

`x-y+1=0`

D

`x-y-1=0`

Text Solution

Verified by Experts

The correct Answer is:
A
`x^2 =4y " " x^2+y^2+6x+8=0`

Line through P and C must be normal
`P(2t,t^2), C(-3,0)`
`x+ty=t^3+2t rArr -3 + 0 = t^3 +2t`
`rArr t^3 + 2t +3 = 0 rArr t=-1 rArr` P(-2,1)
Tangent at P :
`-2x=2(y+1) rArr x+y+1=0`
Promotional Banner

Similar Questions

Explore conceptually related problems

Equation of tangent to the parabola y^(2)=16x at P(3,6) is

Let P be the point on the parabola y^(2) = 4x which is at the shortest distance from the centre S of the circle x^(2) + y^(2) - 4x - 16y + 64 = 0 . Let Q be the point on the circle dividing the lie segment SP internally. Then

If 'P' is any point on the circumference of the circle x^(2) + y^(2) - 4x - 4y -8 =0 , then the perpendicular distance of the tangent at P from the centre of the circle is

If the distance of the point P(x, y) from A(a, 0) is a+x , then y^(2)=?

Let P be the point on parabola y^(2)=4x which is at the shortest distance from the center S of the circle x^(2)+y^(2)-4x-16y+64=0 let Q be the point on the circle dividing the line segment SP internally.Then

Let P be the point on the parabola, y^2=8x which is at a minimum distance from the centre C of the circle,x^2+(y+6)^2=1. Then the equation of the circle, passing through C and having its centre at P is : (1) x^2+y^2-4x+8y+12=0 (2) x^2+y^2-x+4y-12=0 (3) x^2+y^2-x/4+2y-24=0 (4) x^2+y^2-4x+9y+18=0