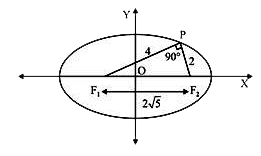
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- F(1) and F(2) are the two foci of the ellipse (x^(2))/(9) + (y^(2))/(4...
Text Solution
|
- If P(x ,y) is any point on the ellipse 16 x^2+25 y^2=400 and f1=(3,...
Text Solution
|
- Let F(1),F(2) are the foci of the ellipse 4x^(2)+9y^(2)=36 and P is a ...
Text Solution
|
- Let d be the perpendicular distance from the centre of the ellipse (x^...
Text Solution
|
- P(x,y) is any point on ellipse 16x^(2)+25y^(2) =400. If F(1)-=(3,0) an...
Text Solution
|
- Let P be a variable on the ellipse (x^(2))/(25)+ (y^(2))/(16) =1 with ...
Text Solution
|
- यदि F(1) (3, 0) और F(2) (-3, 0) दीर्घवृत्त 16x^(2) + 25y^(2) = 400 की ...
Text Solution
|
- If P (x,y) be any point on 16x^(2) + 25y^(2) = 400 with foci F(1)...
Text Solution
|
- F(1) and F(2) are the two foci of the ellipse (x^(2))/(9) + (y^(2))/(4...
Text Solution
|