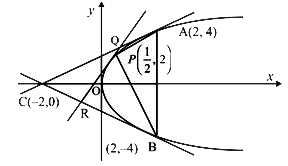
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider the parabola y^(2) = 8x. Let Delta(1) be the area of the tria...
Text Solution
|
- If Delta(1) is the area of the triangle formed by the centroid and two...
Text Solution
|
- Consider the parabola y^(2) = 8x. Let triangle(1) be the area of th...
Text Solution
|
- Consider the parabola y^(2) = 8x. Let Delta(1) be the area of the tria...
Text Solution
|
- If Delta(1) is the area of the triangle formed by the centroid and two...
Text Solution
|
- The area (in sq. units) of the triangle formed by the latus rectum and...
Text Solution
|
- Consider the parabola y^2 = 8x. Let Delta1 be the area of the triangle...
Text Solution
|
- Find the area of the triangle formed by the lines joining the vertex...
Text Solution
|
- y^(2)=8x एक परवलय है। मान लीजिए एक त्रिभुज का क्षेत्रफल है जो नाभिलम्ब...
Text Solution
|