Home
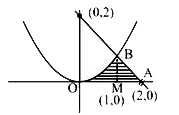
Class 12
MATHS
The area bounded by the curves x+y=2 and...

The area bounded by the curves `x+y=2` and `y=x^2` above x-axis in the first quadrant is ,

A

`(1)/(2)`

B

`(2)/(3)`

C

`(10)/(12)`

D

`(6)/(5)`

Text Solution

Verified by Experts

The correct Answer is:
C
`"Solving "x+y=2& y=x^(2)" "rArr x=-2,1`
`therefore" area of OBAM "=int_(0)^(1)x^(2)dx+int_(1)^(2)(2-x)dx`
`=(1)/(3)+(2x-(x^(2))/(2)):|_(1)^(2)" "=(5)/(6)=(10)/(12)`
Promotional Banner

Similar Questions

Explore conceptually related problems

The area bounded by the curve y=[x],y=x and x=2 is

The area (in sq. units) of the region bounded by the curves y=2^(x) and y=|x+1| , in the first quadrant is :

The area bounded by the curves y=In x,y=|ln x| and the y-axis is

Find the area of the region bounded by the curves x^2 +y^2 =4, y = sqrt(3) x and x- axis in the first quadrant

The area bounded by the curve a^(2)y=x^(2)(x+a) and the x-axis is

The area bounded by the curve x = 4 - y^(2) and the Y-axis is

The area bounded by the curves y=sqrt(x),2y-x+3=0, X-axis and lying in the first quadrant is