Suppose that there are three particles not lying in a straight line so they are taken in a plane.
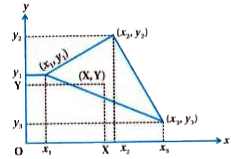
Suppose the coordinates of three particles of masses `m_(1),m_(2)andm_(3)` are `(x_(1),y_(1)),(x_(2),y_(2)) and (x_(3),y_(3))` in two dimension respectively.
If the centre of mass of this system is `(x,y)` then X-coordinate of the centre of mass,
X-coordinate = `(m_(1)x_(1)+m_(2)x_(2)+m_(3)x_(3))/(m_(1)+m_(2)+m_(3))` and
Y-coordinate = `(m_(1)y_(1)+m_(2)y_(2)+m_(3)y_(3))/(m_(1)+m_(2)+m_(3))`
`therefore` Centre of mass,
`(X, Y)=((m_(1)x_(1)+m_(2)x_(2)+m_(3)x_(3))/(m_(1)+m_(2)+m_(3)),(m_(1)y_(1)+m_(2)y_(2)+m_(3)y_(3))/(m_(1)+m_(2)+m_(3)))`
If all three particles having same mass,
`m_(1)=m_(2)=m_(3)=m` assume,
`therefore x`-coordinate of centre of mass,
`X=(mx_(1)+mx_(2)+mx_(3))/(m+m+m)`
`=(x_(1)+x_(2)+x_(3))/(3)` and
y-coordinate `Y=(my_(1)+my_(2)+my_(3))/(m+m+m)`
`=(y_(1)+y_(2)+y_(3))/(3)`
Hence centre of mass of system form by three particles of same mass will be at middle of triangle form by these three particles.
The centre of mass of three particles which are not lying on a line is written as,
Coordinate of C.M.
`(X,Y)=(m_(1)(x_(1),y_(1))+m_(2)(x_(2),y_(2))+m_(3)(x_(3),y_(3)))/(m_(1)+m_(2)+m_(3))`
Coordinate of centre of mass of n particle which are not in line.
`(X,Y)=(m_(1)(x_(1),y_(1))+m_(2)(x_(2),y_(2))+...m_(n)(x_(n),y_(n)))/(m_(1)+m_(2)+...m_(n))`
OR
`(X,Y)=(Sigmam_(i)(x_(i).y_(i)))/(M)`
where `M=Sigmam_(i)` total mass of system and x-coordinate and y-coordinate of centre of mass of system,
`X=(m_(1)x_(1)+m_(2)x_(2)+...m_(n)x_(n))/(m_(1)+m_(2)...m_(n))=(Sigmam_(i)x_(i))/(M)`
and `Y=(m_(1)y_(1)+m_(2)y_(2)+...m_(n)x_(n))/(m_(1)+m_(2)...m_(n))=(Sigmam_(i)y_(i))/(M)`
