The force acting on centre of mass,
`MvecA=vec(F_(1))+vec(F_(2))+...vec(F_(n))" here "vec(F_(1))` is not only one force but it is vector sum of forces acting only a particle.
Similarly for second, third, … .n. particle the vector sum of force actin are `vec(F_(2))+vec(F_(3))+...vec(F_(n))`
The forces acting on particles of a system are of two types :
(i) Internal forces due to mutual interactions among the particles and
(ii) External forces
In the figure (a) a system made of particle-1 and particle-2 is shown.
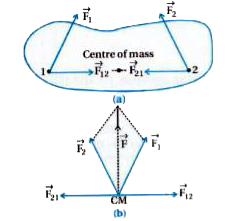
External forces acting on particles 1 and 2 are `vec(F_(1))andvec(F_(2))` respectively and mutual forces interaction are denoted by `vec(F_(12)) and vec(F_(21))`.
Here, all the forces may be considered as acting on the centre of mass which is shown in figure (b).
According to Newton.s third law of motion the internal forces being equal and opposite their resultant is zero. So the force `vecF` acting on the centre of mass can be regarded as resultant external forces only.
`therefore MvecA=vec(F)_(ext)` where `vec(F)_(ext)-vecF` is the resultant force of only external forces.
This equation indicates that the system moves under the effect of resultant external force as if the whole mass of the system where concentrated as its centre of mass.
