In the figure a rigid body is rotating about a fixed axis Oz, normal to the plane of the figure.
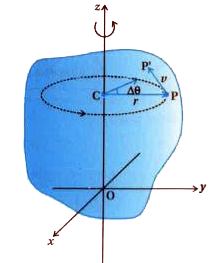
All the particles of a rigid body move along circular path and the centres of all these circles fall on a axis of rotation. Circular path is perpendicular to the axis.
Suppose P is any particle of rigid body. This moves with radius (perpendicular distance from axis) r and about centre C of a circle.
The linear velocity of particle at point P is `vecv` and is in the direction of tangent at point P.
Suppose at `t=0` time particle is at P and at time `t+Deltat` it is on P.
`therefore` angular displacement in `Deltat` time `=anglePCP`
=`Deltatheta`
In this time interval average angular velocity of particle
`ltomegagt =(Deltatheta)/(Deltat)`
As `Deltat` is small and when `Deltat` is near to zero then `(Deltatheta)/(Deltat)` is called instateneous angular velocity
`therefore` Instanteneous angular velocity is known as angular velocity also
`therefore` Angular velocity `omega=underset(Deltatrarr0)lim(Deltatheta)/(Deltat)`
`therefore omega=(d theta)/(dt)`
Defination of angular position : The angle made by the line joining a particle with the centre of its circular path at a given time, with a given fixed reference line is called the angular position of the particle at that time. It is denoted by `theta` and it is scalar.
Angular displacement : The change in angular position of a particle of rigid body is called angular displacement. It is denoted by `Deltatheta`. It is a vector.
Angular velocity : time rate of change of angular position of a rigid body is known as angular velocity or instanteneous angular velocity. It is denoted by `omega` and it is vector.
