The relation between the linear speed and angular speed of particle of rotation motion is `v=romega`, where r is the radius of circular path.
In general by any instant
`v_(i)=r_(i)omega` where `i=1,2,3,….,n` and n is the no. of particles in the rigid body.
If `r=0,v=0`, means particles on axis are stationary.
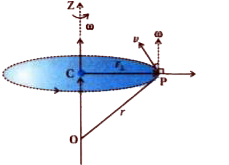
For obtaining the relation between linear velocity and angular velocity, a particle P of a rigid body rotating about Z-axis (fixed) as shown in figure. The position vector `vec(OP)=vecr` of particle at P on the rigid body with respect to the origin O. Its perpendicular distance is `r_(1)` from the centre C circular path.
Now `vecomegaxxvecr=vecomegaxxvec(OP)`
`=vecomegaxx(vec(OC)+vec(CP))`
`=vecomegaxxvec(OC)+vecomegaxxvec(CP)`
but `vecomegaxxvec(OC)=omega(OC)sin0^(@)`
[`because vecomegaandvec(OC)` are in same direction]
= 0
`therefore vecomegaxxvecr=vecomegaxxvec(CP)`
but `vecomega` perpendicular to the radius `vec(CP)` and is parallel to the tangent of circle at P.
`therefore vecomegaxxvecr=vecomegaxxvec(r_(_|_))[because vec(CP)=vec(r_(_|_))]`
`=omegar_(_|_)sin90^(@)`
[`because vecomega and vec(r_(_|_)` are perpendicular]
`=omegar_(_|_)`
but `=omegar_(_|_)` is equal to the magnitude linear velocity at point P
`therefore vecomegaxxvecr=vecv`
Is the relation between angular velocity and linear velocity.
The direction of `vecomega` does not change with time for a rotating body about a fixed time but its magnitude change with time.
It the axis is not remain fixed, direction of angular velocity changes with time.
Hence, in general, for a rotating body the magnitude and direction of `vecomega` changes with time.
