When a rigid body (sphere, circular disc or wheel of vehicle) rolling without slipping then rolling motion exist.
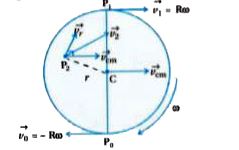
As shown in figure a circular disc of radius R is rolling on its circular surface without slipping.
Its centre of mass is on the geometric centre of the disc `V_(cm)` is the velocity of C. It is parallel to the surface level. The rotational motion of the disc is about axis. Which passes through centre.
`P_(0),P_(1)andP_(2)` are the point on disc is shown in figure the velocity at these points, are obtained the sum of components of vectors.
The resultant velocity at point `P_(1),vec(v_(1))=vec(v_(R))+vec(v_(cm))`
where `vec(v_(R))` is the velocity at `P_(1)` point, `vec(v_(R))=Romega`
`therefore` The resultant velocity at point
`P_(1),vec(v_(1))=Romega+Romega` [`because` are in same direction] [`because` velocity of cm, `vec(v_(cm))=Romega`]
`therefore vec(v_(1))=2Romegaorvec(v_(cm))=2Romega`
The position vector of `P_(2)` is `vecr`. So linear velocity at point `P_(2),vec(v_(r))=rvecomega`, which is perpendicular to position vector `vecr`.
`therefore` The resultant velocity at point
`P_(2)=vec(v_(2))=vec(v_(r))+vec(v_(cm))`
`=vec(r_(omega))+vec(Romega)`
`P_(0)` is instantaneously at rest and the velocity of this point `vec(v_(0))=vec(v_(R))+vec(v_(cm))`, here `v_(0)=0`
`therefore 0=vec(v_(R))+vec(v_(cm))`
but `vec(v_(R))andvec(v_(cm))` are in perpendicular direction
when `|vec(v_(R))|=|-vec(v_(cm))|,P_(0)` becomes at rest.
`therefore` Due to resultant velocity at point `P_(0)` zero,
`v_(cm)=Romega`.
This condition applies to all rolling bodies.
