Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
KUMAR PRAKASHAN|Exercise SECTION-B NUMERICALS FROM TEXTUAL EXERCISE|21 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
KUMAR PRAKASHAN|Exercise SECTION-B ADDITIONAL EXERCISE|12 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
KUMAR PRAKASHAN|Exercise SECTION-A (TRY YOURSELF (VSQs))|94 VideosQUESTIONS ASKED IN JEE - 2020
KUMAR PRAKASHAN|Exercise Question|16 VideosTHERMAL PROPERTIES OF MATTER
KUMAR PRAKASHAN|Exercise Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks|1 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-SECTION-B NUMERICALS
- Show that moment of a couple does not depend on the point about which ...
Text Solution
|
- A metal bar 70 cm long and 4.00 kg in mass supported on two knife-edge...
Text Solution
|
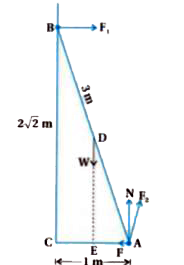
- A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet...
Text Solution
|
- What is the moment of inertia of a disc about one of its diameter?
Text Solution
|
- What is the moment of inertia of a rod of mass M, length l about an ax...
Text Solution
|
- What is the moment of inertia of a ring about a tangent to the circle ...
Text Solution
|
- Obtain equation omega=omega(0)+alphat from first principle.
Text Solution
|
- The angular speed of a motor wheel is increased from 1200 rpm to 3120 ...
Text Solution
|
- A cord of negligible mass is wound round the rim of a fly wheel of mas...
Text Solution
|
- Three bodies, a ring, a solid cylinder and a solid sphere roll down th...
Text Solution
|
- In DeltaABC, mass of 100g, located on point A, mass of 200 g located o...
Text Solution
|
- Find the centre of mass of uniform thin sheet as shown in figure.
Text Solution
|
- Find the centre of mass of uniform thin sheet as shown in figure.
Text Solution
|
- If veca=2hati-hatj-5hatk and vecb=hati+hatj+2hatk, then find scalar an...
Text Solution
|
- If a position vector of a point is vecr=7hati+3hatj+hatk and force act...
Text Solution
|
- Prove that moment of inertia of uniform ring of mass M and radius R ab...
Text Solution
|
- Find the moment of inertia and radius of gyration of uniform cross-se...
Text Solution
|
- Find the moment of inertia and radius of gyration of uniform cross-sec...
Text Solution
|
- Find moment of inertia of a ring of mass 4kg and radius 20cm about its...
Text Solution
|
- Initial angular speed of wheel is 20 rad s^(-1). Its angular displacem...
Text Solution
|