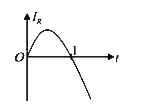
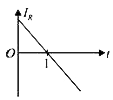
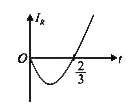A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A long solenoid of radius R carries a time (t)-dependent current I(t)=...
Text Solution
|
- A coil of wire having inductance and resistance has a conducting ring ...
Text Solution
|
- A conducting loop of radius R is present in a uniform magnetic field B...
Text Solution
|
- The diagram given below shows a solenoid carrying time varying current...
Text Solution
|
- a conducting loop of radius R is precent in a uniform magnetic-field B...
Text Solution
|
- A conducting loop of radius R is present in a uniform magnetic field B...
Text Solution
|
- A long solenoid of radius R carries a time dependent current I = I(0) ...
Text Solution
|
- A long solenoid of radius R carries a time (t) – dependent current I=I...
Text Solution
|
- long solenoid of radius R carries a time –dependent current I(t) = I(0...
Text Solution
|