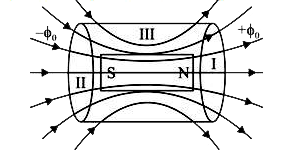
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider a short bar magnet forming a magnetic dipole enclosed by an i...
Text Solution
|
- A current carrying circular loop is placed in an infinite plane if phi...
Text Solution
|
- Consider a short bar magnet forming a magnetic dipole enclosed by an i...
Text Solution
|
- Consider a rectangular coil of wire carrying constant current I, formi...
Text Solution
|
- If the magnetic field is parallel to a surface then, the magnetic flux...
Text Solution
|
- Question based on Magnetic field of a circular arc | Magnetic field of...
Text Solution
|
- Question based on Magnetic field of a solenoid | Magnetic field lines ...
Text Solution
|
- A current carrying circular loop is placed in an infinite plane if phi...
Text Solution
|
- A current carrying circular loop is placed in an infinite plane if phi...
Text Solution
|