Home
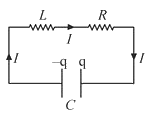
Class 12
PHYSICS
An LCR circuit behaves like a damped har...

An LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:

A

`b harr R`

B

`b harr c`

C

`b harr 1/R`

D

`b harr 1/L`

Text Solution

Verified by Experts

The correct Answer is:
A
For damped oscillation
`ma+bv+kx=0`
`m(d^(2)x)/(dt^(2))+b(dx)/(dt)+kx=0" "(i)`
For LCR series circuit
`-IR-L(dI)/(dt)-(q)/(C)=0`
`L(d^(2)q)/(dt^(2))+R(dq)/(dt)+(q)/(C)=0" "(ii)`
Comparing equation (i) and Equation (ii) `bharrR`
Promotional Banner

Similar Questions

Explore conceptually related problems

An LCR series circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant ‘b’, the correct equivalence would be (Take, i = current, V = voltage, x = displacement, q = charge, F = force, v = velocity)

A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q_(0). then the amplitude of the amount of charge on the capacitor as a function of time t will be:

In a damped harmonic oscillator, periodic oscillations have ………. amplitude.

A LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C^(square) inductor L having resistance R is oscillatory. Then which of following is correct _____.

Damped Harmonic Oscillation|| Forced Harmonic Oscillation

Damped Harmonic Oscillation||Forced Harmonic Oscillation||H.W.-3

If initial amplitude during a damped oscillation of mass m is 12 cm and after 2s it reduces to 6cm then find damping constant(b)

Resonance|| Damped Harmonic Oscillation|| Forced Harmonic Oscillation|| Transformer

A simple harmonic oscillator consists of a particle of mass m and an ideal spring with spring constant k. The particle oscillates with a time period T. The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be

There is a LCR circuit , If it is compared with a damped oscillation of mass m oscillating with force constant k and damping coefficient 'b'. Compare the terms of damped oscillation with the devices in LCR circuit.