A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
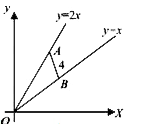
- Let AB be a line segment of length 4 with A on the line y = 2x and B o...
Text Solution
|
- . Find the locus of the middle point of the portion of the line-segmen...
Text Solution
|
- Let AB be a line segment of length 4 with A on the line y=2x and B on ...
Text Solution
|
- Properties of Line segment
Text Solution
|
- The locus of a point which divides a line segment AB=4 cm in 1 : 2, wh...
Text Solution
|
- The projections of a line segment on x,y,z axes are 12, 4, 3. The leng...
Text Solution
|
- The projections of a line segment on x, y and z axes are respectively ...
Text Solution
|
- Let AB be a line segment of length 4 with A on the line y = 2x and B o...
Text Solution
|
- The locus of a point which divides a line segment AB = 4cm in 1:2, whe...
Text Solution
|