Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAVNEET PUBLICATION - MAHARASHTRA BOARD-TRIANGLES-SUMS TO ENRICH REMEMBER
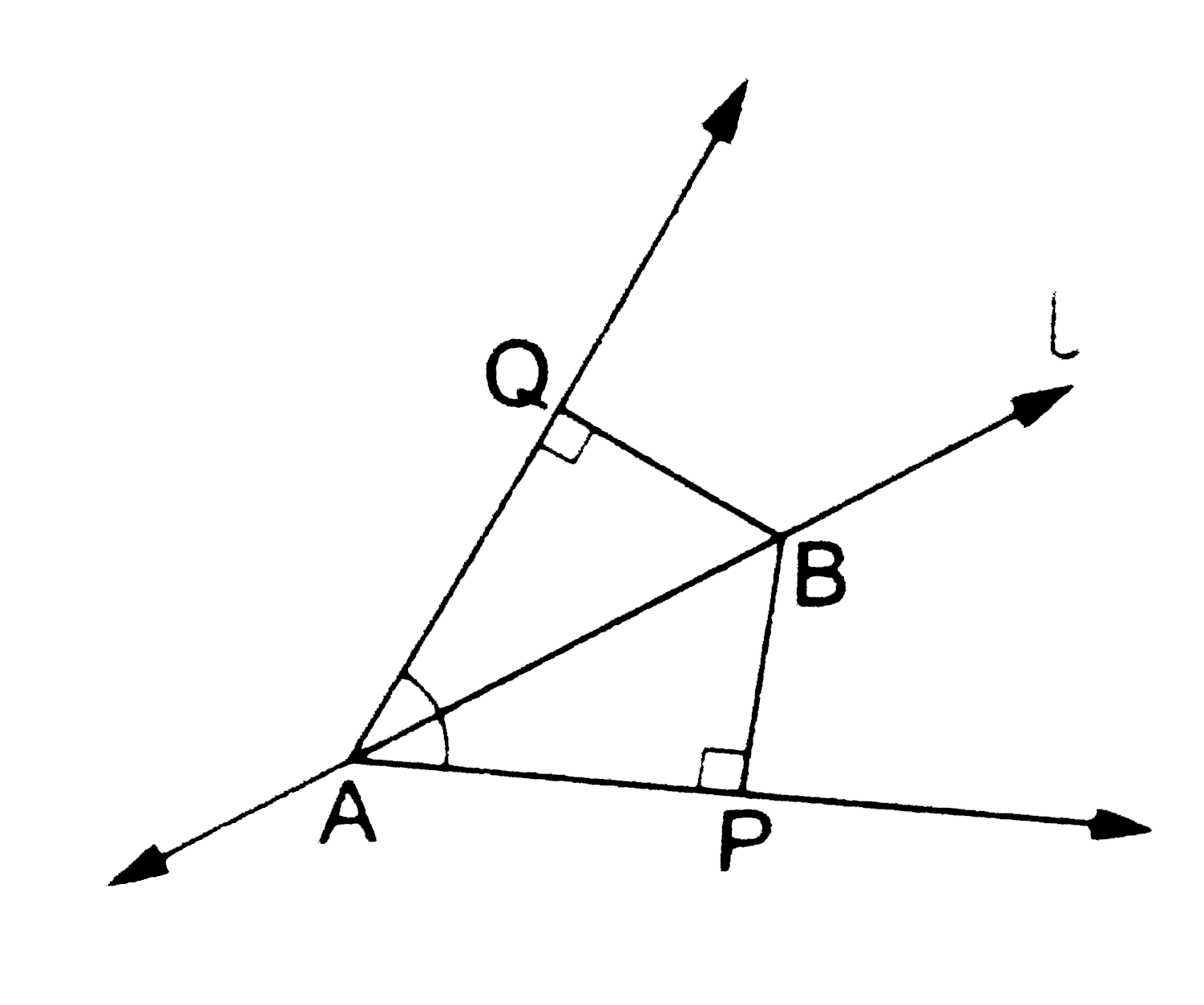
- In the given figure, line l is the bisector of an angle angleA and B ...
Text Solution
|
- In the given figure, OA = OB and OD = OC. Show that (i) DeltaAOD con...
Text Solution
|
- A B is a line segment and line l is its perpendicular bisector. If ...
Text Solution
|
- Line segment AB is parallel to another line segment CD. O is the midpo...
Text Solution
|
- In D ABC, the bisector AD of A is perpendicular to side BC (see...
Text Solution
|
- E and F are respectively the mid-points of equal sides AB and AC of...
Text Solution
|
- In an isosceles DeltaABC with AB = AC, D and E are point on BC such th...
Text Solution
|
- In the given figure, AB is a line segment. P and Q are points on oppos...
Text Solution
|
- P is a point equidistant from two lines l and m intersecting at a poin...
Text Solution
|
- D is a point on side BC of DeltaA B Csuch that A D\ =\ A C(see Fig. 7....
Text Solution
|