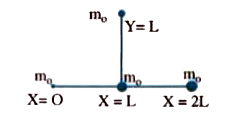Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the centre of mass of the system:
Text Solution
|
- Velocity Of Centre Of Mass Of System
Text Solution
|
- Acceleration Of Centre Of Mass Of System
Text Solution
|
- If the system is released, then the acceleration of the centre of mass...
Text Solution
|
- Calculate centre of mass of the system
Text Solution
|
- If the system is released, then the acceleration of the centre of mass...
Text Solution
|
- Find out the position of centre of mass of two particle system.
Text Solution
|
- Centre of Mass: Basics, finding COM of system of particles
Text Solution
|
- Calculate centre of mass of the system
Text Solution
|