Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
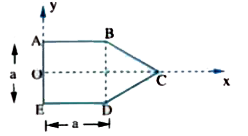
- A uniform lamina ABCDE is made from a square ABDE and an equilaterial...
Text Solution
|
- For the given uniform square lamina ABCD, whose centre is O,
Text Solution
|
- Find the centre of mass of a uniform triangula lamina.
Text Solution
|
- Find the centre of mass of a uniform L shaped lamina (a thin flat plat...
Text Solution
|
- Find the position of centre of mass of the uniform lamina shown in fig...
Text Solution
|
- For the given uniform square lamina ABCD, whose centre is O
Text Solution
|
- A circular hole of diameter 10 cm is punched in a uniform circular lam...
Text Solution
|
- Find the centre of mass of a uniform L-shaped lamina (a thin flat plat...
Text Solution
|
- Find the centre of mass of a triangular lamina.
Text Solution
|