Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
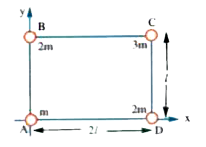
- Four particles of masses m, 2m, 3m and 4m are placed at the vertices o...
Text Solution
|
- Four particles A, B, C and D of masses m, 2m, 3m and 4m respectively a...
Text Solution
|
- The four particles of masses m , 3m, 2m and 4m are placed on the verti...
Text Solution
|
- Four particles of masses m, 2m, 3m, 4m are placed at corners of a squa...
Text Solution
|
- Four particles of masses m, m, 2m and 2m are placed at the four corner...
Text Solution
|
- चार कण A , B , C तथा D जिनके द्रव्यमान क्रमश: m , 2m , 3m तथा 4m है , ...
Text Solution
|
- a भुजा वाले एक वर्ग के चारों कोनों पर m, 2m, 3m तथा 4m द्रव्यमा...
Text Solution
|
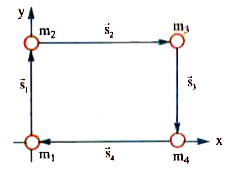
- Four particles A, B, C and D with masses mA = m, mB = 2m, mC = 3m and ...
Text Solution
|
- द्रव्यमान m(A)=m, m(B)=2m, m(C )=3m तथा m(D)=4m वाले चार कण A, B, C और...
Text Solution
|