Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
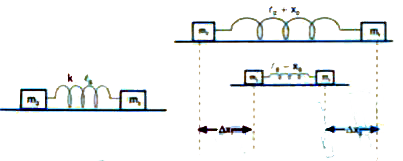
- Two masses m, and m, are connected by a spring of force constant k and...
Text Solution
|
- Two masses m1 and m2 re connected by a spring of spring constnt k and ...
Text Solution
|
- Two blocks m(1) and m(2) are connected by a spring of force constant K...
Text Solution
|
- Two blocks of masses m and m' are connected by a light spring on a hor...
Text Solution
|
- Consider the situations shown in fig (a) and (b) initially the spring ...
Text Solution
|
- A bullted of mass m embeds itself in a block of mass M resting on a sm...
Text Solution
|
- एक घर्षणरहित क्षैतिज सतह पर दो द्रव्यमान m(1) तथा m(2) एक स्प्रग से जो...
Text Solution
|
- A block of mass m is initially moving to the right on a horizontal fri...
Text Solution
|
- Two blocks of masses m, and m, are connected to the ends of a spring o...
Text Solution
|