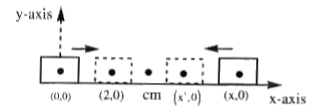Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two particles of masses 10 kg and 30 kg are lying on a straight line. ...
Text Solution
|
- Centre of mass of 3 particles 10 kg, 20 kg and 30 kg is at (0, 0, 0). ...
Text Solution
|
- Two particles of mass 2 kg and 4 kg lie on the same line. If 4 kg is d...
Text Solution
|
- Two particles of masses 10 kg and 30 kg are lying on a straight line. ...
Text Solution
|
- Two particles of masses 10 kg and 30 kg are lying on a stright line. T...
Text Solution
|
- The centre of mass of three particles of masses 10 kg, 20 kg and 30 kg...
Text Solution
|
- Two blocks of masses 10 kg and 30 kg are placed on x - axis. The first...
Text Solution
|
- If the centre of mass of three particles of masses of 1 kg, 2 kg, 3 kg...
Text Solution
|
- Two particles of masses 10kg and 30kg are lying on a straight line. Th...
Text Solution
|