Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
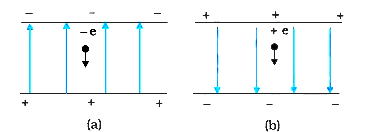
- An electron falls throgh a distance of 1.5 cm in a uniform electric f...
Text Solution
|
- An electron falls through a small distance in a uniform electric field...
Text Solution
|
- An electron falls through a distance of 1.5 cm in a uniform electri...
Text Solution
|
- An electron falls through a distance of 1.5 cm in a uniform electric f...
Text Solution
|
- An electron initially at rest falls a distance of 1.5 cm in a uniform ...
Text Solution
|
- An electron falls through a distance of 1.5 cm in a uniform electric f...
Text Solution
|
- कोई इलेक्ट्रॉन विरामावस्था से किसी एकसमान तथा। ऊपर की ओर ऊध्याधर C विद...
Text Solution
|
- An electron falls through distance of 1.5 cm in a uniforth electric fi...
Text Solution
|
- An electron falls throgh a distance of 1.5 cm in a uniform electric fi...
Text Solution
|