Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT TAMIL-OSCILLATIONS-EVALUATION(IV. NUMERICAL PROBLEMS)
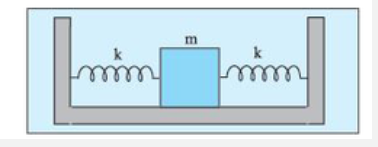
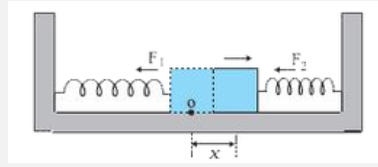
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- Calculate the time period of the oscillation of a particle of mass m m...
Text Solution
|
- Consider two simple harmonic motion along x and y-axis having same fre...
Text Solution
|
- Show that for a particle executing simple harmonic motion a. the ave...
Text Solution
|
- Compute the time period for the following system if the block of mass ...
Text Solution
|