Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
AAKASH SERIES-MOTION IN A PLANE -Practice Exercise
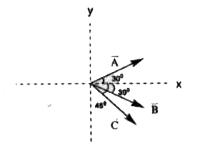
- Three vectors vec(A), vec(B), vec(C) are shown in the figure. Find ang...
Text Solution
|
- A person runs along a circular path of radius 5m. Find the magnitude o...
Text Solution
|
- A car is moving 40 m due east, turns towards north moves 30 m, then tu...
Text Solution
|
- If vec(A) = 3hat(i) - 4hat(j) and vec(B) = -hat(i) - 4hat(j), calculat...
Text Solution
|
- The resultant of the forces vec(F)(1) = 4hat(i) - 3hat(j) and vec(F)(2...
Text Solution
|
- The horizontal and vertical components of a force re 8 N and 15 N resp...
Text Solution
|
- An aeroplane is heading north east at a speed of 141.4ms^(-1). The nor...
Text Solution
|
- To go from town A to ton B a plane must fly about 1780 km at an angle ...
Text Solution
|
- A wheel of perimeter 4pi m is rolling on a horizontal surface. The dis...
Text Solution
|
- Given two vectors vec(A) = hat(i) - 2hat(j) - 3hat(k) and vec(B) = 4ha...
Text Solution
|
- If the two directional cosines of a vectors are (1)/(sqrt(2)) and (1)/...
Text Solution
|
- If vec(P) = hat(i) + hat(j) + hat(k), its direction cosines are
Text Solution
|
- If vec(A) = 2hat(i) - 3hat(j) + 4hat(k) its component in xy plane is
Text Solution
|
- The unit vector parallel to the resultant of the vectors vec(A) = 4hat...
Text Solution
|
- A vector hat(i) + sqrt(3) hat(j) rotates about its tail through an ang...
Text Solution
|
- If the angle between two vectors of equal magnitude P is theta, the ma...
Text Solution
|
- Two forces are in the ratio of 5:2. The maximum and minimum of their r...
Text Solution
|
- Two equal forces of magnitude .p. each are angled first at 60^(@) late...
Text Solution
|
- Three vectors vec(P), vec(Q), vec(R) obey vec(P) + vec(Q) = vec(R) and...
Text Solution
|
- The resultant of two forces 2 N and 3 N is sqrt(19) N. The angle betw...
Text Solution
|
- Twelve forces each of 5 N act on a body simultaneously. If each force ...
Text Solution
|