Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
AAKASH SERIES-GRAVITATION-ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
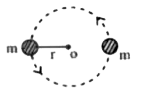
- Two particles of equal mass move in a circle of radius r under the act...
Text Solution
|
- Assume the planetary orbits to be circular and T be the time period o...
Text Solution
|
- A planet revolves about the sun in elliptical orbit of semimajor axis ...
Text Solution
|
- the proper potential Energy of gravitation interaction of matter (i.e ...
Text Solution
|
- A satellite is launched in the equatorial pane in such a way that it c...
Text Solution
|
- The minimum colatitude which can directly receive a signed from a geos...
Text Solution
|
- The gravitational field in a region is given by vecE = (5hati + 12hatj...
Text Solution
|