Topper's Solved these Questions
LINE AND ANGLES
KUMAR PRAKASHAN|Exercise Skill Testing Exercise|21 VideosLINE AND ANGLES
KUMAR PRAKASHAN|Exercise Multiple Choice Questions MCQs)|10 VideosLINE AND ANGLES
KUMAR PRAKASHAN|Exercise EXERCISE 6.3|6 VideosINTRODUCTION TO EUCLID'S GEOMETRY
KUMAR PRAKASHAN|Exercise MULTIPLE CHOICE QUESTIONS|3 VideosLINEAR EQUATIONS IN TWO VARIABLES
KUMAR PRAKASHAN|Exercise Multiple Choice Questions (MCQs)|7 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-LINE AND ANGLES-Sums of Enrich Remember.s
- In the given figure, lines PQ and RS intersect each other at point O. ...
Text Solution
|
- In the given figure, ray OS stands on a lien POQ. Ray OR and ray OT ar...
Text Solution
|
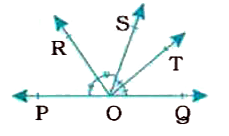
- In the given figure, OP, OQ, OR and OS are four rays. Prove that ang...
Text Solution
|
- In the given figure 1, if PQ||RS,angleMXQ=135^(@) and angleMYR=40^(@),...
Text Solution
|
- If a transversal intersects two lines such that the bisectors of a pai...
Text Solution
|
- In the given figure, AB||CD and CD||EF Also EAbotAB. If angleBEF=55^(@...
Text Solution
|
- In the given figure, if QTbotPR,angleTQR=40^(@) and angleSPR=30^(@), f...
Text Solution
|
- In the adjacent figure the sides AB and AC of Delta ABC are produced t...
Text Solution
|