Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-TRIANGLES-EXERCISE 7.2
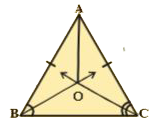
- In an isosceles triangle ABC, with AB = AC, the bisectors of / B and /...
Text Solution
|
- In triangle ABC, AD is the perpendicular bisector of BC (see the given...
Text Solution
|
- ABC is an isosceles trian gle in w h ich altitudes BE and CF are drawn...
Text Solution
|
- ABC is a triangle in which altitudes BE and CF to sides AC and AB are ...
Text Solution
|
- ABC and DBC are two isosceles triangles on the same base BC (see the g...
Text Solution
|
- triangle ABC is an isosceles tr ia n g le in w h ich AB = AC. Side BA ...
Text Solution
|
- ABC is a right angled triangle in which angle A = 90^(@) and AB = AC. ...
Text Solution
|
- Show that the angles of an triangle are 60^(@) each.
Text Solution
|