Home
Class 10
MATHS
In the given figure, ABC and AMP are two...

In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
`DeltaABC ~ DeltaAMP`

Text Solution

Verified by Experts

The correct Answer is:
AA criterion, `DeltaABC ~ DeltaAMP`.
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    KUMAR PRAKASHAN|Exercise EXERCISE 6.4|9 Videos

  • TRIANGLES

    KUMAR PRAKASHAN|Exercise EXERCISE 6.5|23 Videos

  • TRIANGLES

    KUMAR PRAKASHAN|Exercise EXERCISE 6.2|12 Videos

  • SURFACE AREAS AND VOLUMES

    KUMAR PRAKASHAN|Exercise TEST YOUR SKILLS|5 Videos

Similar Questions

Explore conceptually related problems

In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that : (CA)/(PA)=(BC)/(MP)

Delta ABC and Delta AMP are two right triangles right angled at B and M respectively. Prove that (i) Delta ABC ~ Delta AMP and (ii) (CA)/(PA) = (BC)/(MP) .

In the given figure, DeltaABC is a right angled Deltawith /_B= 90^(@) and BD is perpendicular to AC. Prove that DeltaADB ~ DeltaABC

In the given figure, ABC is a triangle right angled at B. D and E are ponts on BC trisect it. Prove that 8AE^(2) = 3AC^(2) + 5AD^(2) .

In the given figure, ABC is a right triangle, right angled at A. AB = 3 cm and AC = 4 cm. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region.

In the given figure, ABD is a triangle right angled at A and AC bot BD . Show that AC^(2)= BC*DC

In the given figure, ABD is a triangle right angled at A and AC bot BD . Show that AD^(2)= BD*CD

In the given figure ABC is a right triangle and right angled at B such that /_BCA = 2/_BAC. Show that hypotenuse AC = 2BC.

In the given figure, ABC and DBC are two triangles on the same base BC. Prove that (ar(ABC))/(ar(DBC))= (AO)/(DO) .

ABC and ADC are two right triangles with common hypotenuse AC. Prove that angle CAD = angle CBD.

KUMAR PRAKASHAN-TRIANGLES-EXERCISE 6.3
  1. Digonal AC and BD of a trapezium ABCD with AB||DC intersects each othe...

    Text Solution

    |

  2. In the given figure (QR)/(QS)=(QT)/(PR)" and "/1= /2. Show that DeltaP...

    Text Solution

    |

  3. S and T are points on sides PR and QR of DeltaPQR such that /P= /RTS. ...

    Text Solution

    |

  4. In the given figure, if DeltaABE cong DeltaACD, show that DeltaADE ~ D...

    Text Solution

    |

  5. In the given figure, altitudes AD and CE of DeltaABC intersect each ot...

    Text Solution

    |

  6. In the given figure, altitudes AD and CE of DeltaABC intersect each ot...

    Text Solution

    |

  7. In the given figure, altitudes AD and CE of DeltaABC intersect each ot...

    Text Solution

    |

  8. In the given figure, altitudes AD and CE of DeltaABC intersect each ot...

    Text Solution

    |

  9. E is a point on the side AD produced of a parallelogram ABCD and BE in...

    Text Solution

    |

  10. In the given figure, ABC and AMP are two right triangles, right angled...

    Text Solution

    |

  11. In the given figure, ABC and AMP are two right triangles, right angled...

    Text Solution

    |

  12. CD and GH are respectively the bisectors of /ACB" and "/EGF such that ...

    Text Solution

    |

  13. CD and GH are respectively the bisectors of /ACB" and "/EGF such that ...

    Text Solution

    |

  14. CD and GH are respectively the bisectors of /ACB" and "/EGF such that ...

    Text Solution

    |

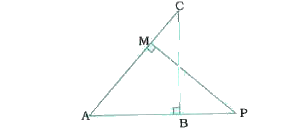
  15. In the given figure, E is a point on side CB produced of an isosceles ...

    Text Solution

    |

  16. Sides AB and BC and median AD of a DeltaABC are respectively proportio...

    Text Solution

    |

  17. D is a point on the side BC of a triangle ABC such that /ADC= /BAC. Sh...

    Text Solution

    |

  18. Sides AB and BC and median AD of a DeltaABC are respectively proportio...

    Text Solution

    |

  19. A vertical pole of length 6 m casts a shadow 4 m long on the ground an...

    Text Solution

    |

  20. If AD and PM are medians of triangles ABC and PQR respectively , where...

    Text Solution

    |