Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-TRIANGLES-EXERCISE 6.4
- Let DeltaABC ~ DeltaDEF and their areas be, respectively, 64cm^(2) and...
Text Solution
|
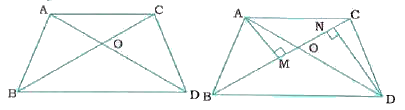
- Digonals of a trapezium ABCD with AB||DC intersect each other at the p...
Text Solution
|
- In the given figure, ABC and DBC are two triangles on the same base BC...
Text Solution
|
- If the areas of two similar triangles are equal, prove that they are c...
Text Solution
|
- D, E and F are respectively the mid-points of sides AB, BC and CA of D...
Text Solution
|
- Prove that the ratio of the areas of two similar triangles is equal to...
Text Solution
|
- Prove that the area of an equilateral triangle described on one side o...
Text Solution
|
- ABC and BDE are two equilateral triangles such that D is the mid-point...
Text Solution
|
- Sides of two similar triangles are in the ratio 4 : 9. Areas of these ...
Text Solution
|