Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
COORDINATE GEOMETRY
KUMAR PRAKASHAN|Exercise Exercise 7 . 4|8 VideosCOORDINATE GEOMETRY
KUMAR PRAKASHAN|Exercise Test Your Skills|23 VideosCOORDINATE GEOMETRY
KUMAR PRAKASHAN|Exercise Exercise 7 . 2|10 VideosCONSTRUCTIONS
KUMAR PRAKASHAN|Exercise OBJECTIVE QUESTIONS|25 VideosINTRODUCTION TO TRIGONOMETRY
KUMAR PRAKASHAN|Exercise Objective Questions|24 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-COORDINATE GEOMETRY-Exercise 7 . 3
- Find the area of the triangle whose vertices are : (1) (2,3), (-1, 0...
Text Solution
|
- In each of the following find the value of 'k', for which the points...
Text Solution
|
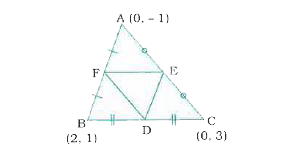
- Find the area of the triangle formed by joining the midpoints of the ...
Text Solution
|
- Find the area of the quadrilateral whose vertices, taken in order, ar...
Text Solution
|
- You have studied in Class IX, (Chapter 9, Example 3), that a median of...
Text Solution
|