Text Solution
Verified by Experts
Topper's Solved these Questions
WORK, ENERGY AND POWER
KUMAR PRAKASHAN|Exercise SECTION - C Objective Questions (VSQs)|52 VideosWORK, ENERGY AND POWER
KUMAR PRAKASHAN|Exercise SECTION - D NCERT Exemplar Solutions (Multiple Choice Questions)|21 VideosWORK, ENERGY AND POWER
KUMAR PRAKASHAN|Exercise SECTION - B Numericals (Numerical From Textual Exercise)|42 VideosWAVES
KUMAR PRAKASHAN|Exercise SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)|23 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-WORK, ENERGY AND POWER -SECTION - B Numericals (Numerical From .DARPAN. Based On Textbook)
- A body while being acted upon by a force vec(F )(x)=(3x^(2)-2x+7)hat(i...
Text Solution
|
- A body of mass 2 kg is rest on a smooth horizontal surface . When a ho...
Text Solution
|
- A block of mass 1 kg falls freely on a spring form a height of 20 c...
Text Solution
|
- A particle of mass m moves on a circular path of radius r . Its cent...
Text Solution
|
- A ball moving with a velocity of 12ms^(-1) collides with another ide...
Text Solution
|
- A tube is fixed in a vertical plane as shown in figure .Form point A a...
Text Solution
|
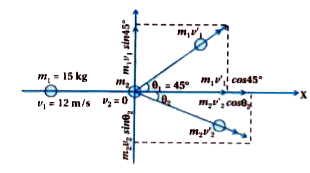
- A sphere of steel of mass 1 kg moving with a velocity of 12m/s ,along ...
Text Solution
|
- The relation between position and time f for a particle , performing ...
Text Solution
|
- A spring of force constant k is kept in the compressesd condition bet...
Text Solution
|
- Two beads of masses m(1) and m(2) are closed threaded on a smooth c...
Text Solution
|
- A bullet is fired into a huge wooden block . The bullet while moving ...
Text Solution
|
- Force F on the particle of mass 0.1 kg varies with distance x as shown...
Text Solution
|
- Work done by a body is shown as in figure . Calculate the work done du...
Text Solution
|
- The centripetal force on a particle moving in a uniform circular moti...
Text Solution
|
- By increasing the volume of water coming out per second the water p...
Text Solution
|