Home
Class 11
PHYSICS
A ball of mass m , moving with a speed 2...

A ball of mass m , moving with a speed `2v_(0)` collides inelastically `( e gt 0)` with an identical ball at rest . Show that
(a) For head - on collision , both the balls move forward .
(b) For a general collision , the angle between the two velocities of scattered balls is less than `90^(@)`

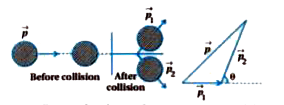
Text Solution

Verified by Experts

(a) Let `v_(1) and v_(2)` are velocities of the two balls after collision .
From law of conservation of linear momentum ,
`2mv_(0)=mv_(1)+mv_(2)`
` :. 2v_(0) =v_(1)+v_(2)`
and `e= (v_(2)-v_(1))/(2v_(0)) rArr v_(2)=v_(1) +2v_(0)e`
` :. 2v_(1)=2v_(0)-2ev_(0)`
` :. v_(1)=v_(0)(1-e)`
Since , `e lt 1 rArr v_(1)` has the same sign as `v_(0)` therefore , the ball moves on after collision .
(b) Consider the diagram below for general collision .

From the law of conservation of linear momentum ,
`P=P_(1)+P_(2)`
For inelastic collision some KE is lost , hence
`(p^(2))/(2m)gt(p_(1)^(2))/(2m)+(p_(2)^(2))/(2m)`
`p^(2)gt p_(1)^(2)+p_(2)^(2)`
Thus , p,`p_(1) and p_(2)` are related as shown in the figure.
`theta` is acute (less than `90^(@)`)
`(p^(2)=p_(1)^(2)+p_(2)^(2) "would be given if " theta =90^(@))`
Promotional Banner

Topper's Solved these Questions

  • WORK, ENERGY AND POWER

    KUMAR PRAKASHAN|Exercise SECTION - D NCERT Exemplar Solutions (Long Answer Type Questions)|5 Videos

  • WORK, ENERGY AND POWER

    KUMAR PRAKASHAN|Exercise SECTION - E Multiple Choice Questions (MCQs)|64 Videos

  • WORK, ENERGY AND POWER

    KUMAR PRAKASHAN|Exercise SECTION - D NCERT Exemplar Solutions (Very Short Answer Type Questions)|12 Videos

  • WAVES

    KUMAR PRAKASHAN|Exercise SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)|23 Videos

Similar Questions

Explore conceptually related problems

A spherical ball of mass 1 kg moving with a uniform speed of 1 m//s collides symmetrically with two identical spherical balls of mass 1 kg each at rest touching each other. If the two balls move with 0.5 m//s in two directions at the same angle of 60^(@) with the direction of the first ball, the loss of kinetic energy on account of the collision is :-

For a ball of mass 0.12 kg and moving with speed of 20 m/s .Calculate de-Broglie wave length.

A ball moving with a velocity of 12ms^(-1) collides with another identical stationary ball . After the collision they move as shown in figure . Find the speed of the balls after the collision . Also , decide whether the condition is elastic or not .

A ball A moving with a velocity 5 m/s collides elastically with another identical ball at rest such that the velocity of A makes an angle of 30^(@) with the line joining the centres of the balls. Then consider following statements : (A) Balls A an B move at right angles after collision (B) kinetic energy is conserved (C) speed of A after collision is (5/2) m/s (D) speed of B after collision is ( 5sqrt(3)//2 ) m/s Select correct alternative :-

A ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient os restitution is 2/3. Find the velocities of both ball after the collision.

A massive ball moving with speed v collieds with a tiny ball which is intially at rest having a mass very much smaller than the mass of the first ball. The collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to :-

On a frictionless surface , a block of mass . M moving at speed v collides elastically with another block of same mass M which is intially at rest /After collision the first block moes at an angle theta to its initial direction and has a speed v/3 The second block's speed after the collision is :

Two balls of masses m_(1), m_(2) and speeds v_(1) and v_(2) collide at right angle . The maximum amount of kinetic energy loss due ot inelastic collision is ___.

A mass 'm' moves with a velocity 'v' and collides inelastieally with another identical mass . After collision the 1^(st) mass moves with velocity v/sqrt3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2^(nd) mass after collision. undersetunderset ((before),(collision))(m)(*rarr) underset(m)* uparrow v//sqrt3 underset((after),(collision):)

After a completely inelastic collision two objects of the same mass and same initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.